|
|
The Cerenkov counters also differ in size and form. These attributes depend on the practical necessities. Invariably all of them use the Cerenkov effect to detect and to identify particles. They work when the particles have velocities close to the velocity of light in the vacuum.
The Cerenkov effect is the following: When particles move in a material medium with a velocity greater than the velocity of the light in the medium, part of the emitted light by the excited atoms appears in form of coherent wave front at a fixed angle with respect to the particle trajectory. The angle at which the coherent front of waves appears, is directly related with the velocity of the particle.
From the Figure 10, it is possible to write:
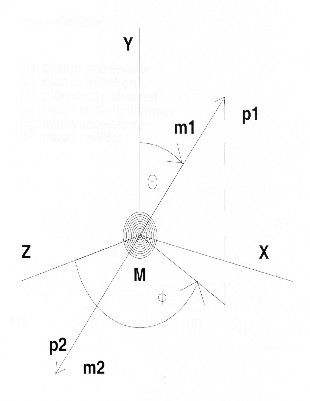
with ![]() the medium refraction index,
the medium refraction index,
then
The angle ![]() is fixed, if
is fixed, if ![]() is fixed. Therefore, measuring the angle that the
coherent wave front makes with the direction of the moving particle, it is possible to
determine the velocity of the particle in the medium.
is fixed. Therefore, measuring the angle that the
coherent wave front makes with the direction of the moving particle, it is possible to
determine the velocity of the particle in the medium.