


Next: The Experimental High energy
Up: The Precepts of Physics
Previous: 2.2.2 The Quantum Precepts
Example:
We can take the case of the black body radiation. That is, the experimental distribution
of the black body radiation intensity as a function of the frequency of the radiation.
A black body is a physical system that, in thermal equilibrium, emits radiation at the same rate
that receives it. A metallic black plaque is a good approximation, the sun or another star is another
good example, the entire universe is perhaps the best of all of them. None of them is
useful in the school laboratory.
The experimental device in the laboratory is a metallic cavity. It can have the size of a regular
orange. And to let the radiation get out has a some millimetre diameter hollow.
The physicists also measure the distribution of the emitted radiation by the sun, or another
star, and the background radiation of the entire universe. This distribution of the radiation
is already given at a fixed temperature, since the sun or the cooled universe are at some
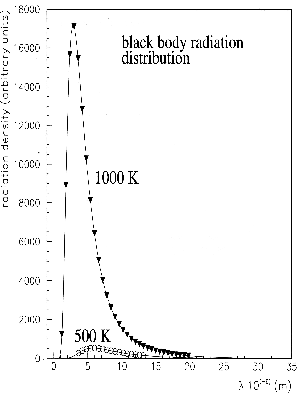
fixed temperature. The physicists can not change it. The Figure 3
shows the distribution of the background radiation of the entire universe. On
the other hand, the physicist can manipulate the temperature of the cavity,
and obtain the curves of distribution at different temperatures. See Figure 3
and Figure 4.
In the black body, the physicists can study the thermal equilibrium between the
electromagnetic radiation and the atoms of the cavity. The study lets answer the
question: How is the interchange of energy between the atoms of the black body and the
electromagnetic field? The physicists obtain the experimental results after
years of efforts. These are presented in the form of curves of distribution; the
intensity of the radiation the physicist lay it in the vertical axis and the wave length of
radiation in the horizontal axis.
The experimental curve of the intensity of the radiation begins at zero at wave length zero,
as can be seen from the extrapolation. At a given temperature (example 500  ), when the wave length
increases the radiation intensity increases; the radiation intensity reaches a maximum and
decreases. Asymptotically the intensity of the radiation goes to zero when the wave length
of the radiation becomes big. At another temperature (example 1000
), when the wave length
increases the radiation intensity increases; the radiation intensity reaches a maximum and
decreases. Asymptotically the intensity of the radiation goes to zero when the wave length
of the radiation becomes big. At another temperature (example 1000  ), the distribution
of the radiation intensity reaches a maximum at shorter wave length. See Figures 3 and 4.
), the distribution
of the radiation intensity reaches a maximum at shorter wave length. See Figures 3 and 4.
Figure 2:
The entire universe as a black body.
|
|
Figure 3:
Black body radiation distribution.
|
|
Figure:
Black body radiation distribution at two different temperatures. The fit to the expression
 is super imposed.
is super imposed.
|
|
When the physicists began the studies of the black body radiation, they counted on the
classical mechanics, the classical electromagnetic theory, and the classical
thermodynamics. Raleigh and Jeans in England, each one by his own efforts, tried
to solve the problem using the electromagnetic theory.
The result was a catastrophe. A big disaster. From the classical electromagnetic point of view,
the radiation propagates continuously. -the radiation behaves like a wave-;
therefore the most natural is to consider that the interchange of radiation, between
the electromagnetic field and the atoms of the black body radiation, is carried continuously.
So Raleigh and Jeans assumed it. The calculations based on the electromagnetic theory
were in frank disagreement with the experimental curves. That is, the electromagnetic theory
conducts to erroneous predictions. This is, the electromagnetic theory can not explain
the black body radiation distribution. Neither the classical thermodynamics can
explain it, as we will show in the next paragraphs.
Planck in Germany tried to solve the same problem using the classical thermodynamics.
After many failures, and about four years of efforts following essentially the
same hypothesis about the interchange of energy that Raleigh and Jeans had followed, Planck
tried a desperate hypothesis. He supposed that the radiation is interchanged discontinuously.
Planck quantized the form in which the electromagnetic radiation is
interchanged with the atoms of the black body. The success was immediate. The theoretical
prediction agree spectacularly with the measurements. The solution of the problem lead
to a deep revolution on the knowledge about the nature.
Planck wrote in his autobiography:
The problem was in finding a formula for R so that it would lead to the
law of energy distribution established by the measurements. In consequence,
it was evident that for the general case it had to obtain that the quantity R
be equal to the sum of one term proportional at the first power of the energy
and of another one proportional to the second power of the energy so that the
first term were decisive at small values of the energy and the second term
were significant at bigger values. In this way I got a formula for the
radiation that I presented for study at the 19 October 1900 meeting of the
Physical Society of Berlin.
And he follows:
The next morning I got the visit of my colleague Rubens, who came to tell me that
the night before, after knowing my conclusions presented at the meeting, he had compared
my formula with his measurements and he had discovered a good agreement in all points.
Also Lummer and Pringsheim, who at the beginning believed that they had found divergences,
retired their objections because, according
with what Pringsheim told me, the divergences that they had observed were for an error
in the calculations. Besides, the measurements performed later confirmed time after time my
formula of the radiation; while more refined were the applied methods, more exact
resulted the formula.
The following developments are very instructive. Max Planck writes:
But, even when the absolute precise validity of the formula of the radiation were
established, while it had merely the credit of being a discovered law by fortunate intuition,
we could not hope that it had more than a formal significance. For this reason, the same day
I formulated the before mentioned law I dedicated myself to investigate its real physical
significance, that leaded me automatically to the study of the interrelation of the
entropy with the probability, in other words, to continue developing the Boltzmann ideas.
For the entropy 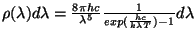 is an additive magnitude, while the probability
is an additive magnitude, while the probability  is
multiplicative, simply I postulated that
is
multiplicative, simply I postulated that 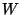 , where
, where  is a universal constant,
and I investigated if the formula for
is a universal constant,
and I investigated if the formula for 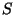 , that is obtained when
, that is obtained when 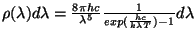 is replaced by
the corresponding value from the law before mentioned, could be interpreted as a measure of
the probability.
is replaced by
the corresponding value from the law before mentioned, could be interpreted as a measure of
the probability.
See Figure 3 and 5. There, in each case, it is superimposed the Planck proposed distribution to the
data distribution. The student must conclude by himself or herself, after studying
deeply the coincidence between the measurements and the given values from the Planck theoretical
expression.
And in other paragraph he continues:
Now, in the case of the magnitude 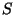 , I discovered that to interpret it
as a probability it was necessary to introduce a universal constant, that I
denominated
, I discovered that to interpret it
as a probability it was necessary to introduce a universal constant, that I
denominated 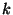 . Because this constant has action dimensions (energy multiplied by time)
I christened it as
. Because this constant has action dimensions (energy multiplied by time)
I christened it as
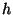 . Hence, the nature of the
entropy as a measure of probability, in the sense indicated by Boltzmann, was established
also in the dominion of the radiation.
. Hence, the nature of the
entropy as a measure of probability, in the sense indicated by Boltzmann, was established
also in the dominion of the radiation.
And about the physical significance of 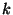 Planck wrote:
Planck wrote:
Even the physical significance of the elementary quantum of action for the
interrelation of the entropy and probability was established conclusively, regardless the
role played by this new constant in the regular and uniform course of the physical process,
the constant was still an unknown. In consequence, immediately I tried to unify
in some way the elementary quantum of action 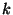 with the frame of the theoretical classical theory.
But in all tries, the constant was inflexible. Always that it were considered as
infinitely small -e.g., when we treat with higher energies and longer periods of time- every
thing went fine. However, in the general case, the difficulties popped up in one corner or other
and became more notorious at high frequencies. Because the failure to solve this
obstacle, it became evident that the elementary quantum of action has fundamental importance
in atomic physics and that its introduction inaugurated a new epoch in the natural science,
because announced the advents of something without precedents which was destined to
redesign fundamentally all perspectives of the physics and the human thought that, since the
epoch when Newton and Leibniz laid the foundations of the infinitesimal calculus, were based on
the supposition that all causal interactions are continuous.
with the frame of the theoretical classical theory.
But in all tries, the constant was inflexible. Always that it were considered as
infinitely small -e.g., when we treat with higher energies and longer periods of time- every
thing went fine. However, in the general case, the difficulties popped up in one corner or other
and became more notorious at high frequencies. Because the failure to solve this
obstacle, it became evident that the elementary quantum of action has fundamental importance
in atomic physics and that its introduction inaugurated a new epoch in the natural science,
because announced the advents of something without precedents which was destined to
redesign fundamentally all perspectives of the physics and the human thought that, since the
epoch when Newton and Leibniz laid the foundations of the infinitesimal calculus, were based on
the supposition that all causal interactions are continuous.
And Planck was right. When physicists got the quantum image of nature and
the laws for the quantum, the physics changed and the physical image of the universe too.
And in consequence, the society. We will speak more about these themes in Section 4.
As a consequence of these new knowledges, the society got a huge number of new
tools; the transistor is an instance; the chip is another one. The microwave
oven another. The physicists increase the borders of the knowledge using the new
mechanics. They understand the nature of the X rays, the emission of particles, etc.
As the reader can appreciate from the above sections, the process of theorization
and the process of experimentation do not oppose each other; the history of Planck
is a great example; those are processes that reinforce and feedback each other. They correct
each other and enrich our image of the universe. When they do so, they make our
knowledge on the nature go forward.
The physicists have corrected the ideas in physics, many times, using the
experimental method; Galileo Galilei corrected the Aristotelian ideas about
the laws of mobile bodies; A. Michelson corrected the ideas about
space and ether of the classical electrodynamics. Each of those corrections
pushed physics forward; and opened new perspectives in the physics.
The physics is an experimental science. This is an unavoidable truth. For the
physicists understand the world it is indispensable that he has a perceptual image
created and supported by the experimental evidence. A collection of experimental data
does not give us an image about the universe. In the same way, a collection of axioms,
without the experimental support, neither give us an image about the external world.
The image of the world is constructed on the experimental and axiomatical truth.
The axioms must be supported by the most complete experimental evidence.



Next: The Experimental High energy
Up: The Precepts of Physics
Previous: 2.2.2 The Quantum Precepts
root
2001-01-22
 ), when the wave length
increases the radiation intensity increases; the radiation intensity reaches a maximum and
decreases. Asymptotically the intensity of the radiation goes to zero when the wave length
of the radiation becomes big. At another temperature (example 1000
), when the wave length
increases the radiation intensity increases; the radiation intensity reaches a maximum and
decreases. Asymptotically the intensity of the radiation goes to zero when the wave length
of the radiation becomes big. At another temperature (example 1000  ), the distribution
of the radiation intensity reaches a maximum at shorter wave length. See Figures 3 and 4.
), the distribution
of the radiation intensity reaches a maximum at shorter wave length. See Figures 3 and 4.
![\includegraphics[width=3.5in,height=2.7in]{felix6.eps}](img16.gif)
 is super imposed.
is super imposed.![\includegraphics[width=2.7in,height=3.5in]{felix7.eps}](img17.gif)