| (32) |
But DM does not seem the end of the story regarding the energy of the
universe. There is a growing evidence that the energy is the critical one
| (32) |
This constant ![]() had been introduced by Einstein in his equations in
a way equivalent to add to the energy-momentum tensor Eq.(2) a term
had been introduced by Einstein in his equations in
a way equivalent to add to the energy-momentum tensor Eq.(2) a term
| (33) |
Now, with Eqs.(3), (4) and (32), the deceleration parameter is
| (34) |
The existence of a cosmological constant leads to an agreement between the
relative large age of the universe and large present Hubble parameter ![]() because it acts as opposing the effect of gravitational attraction. Another
impressive evidence is the fit of the so-called acoustic peak of the
anisotropy of CBR which favours
because it acts as opposing the effect of gravitational attraction. Another
impressive evidence is the fit of the so-called acoustic peak of the
anisotropy of CBR which favours ![]() and
and ![]() , issue
that will be completely settled by the future satellites MAP and Planck.
, issue
that will be completely settled by the future satellites MAP and Planck.
It is interesting(14) that also the reionization of intergalactic
matter,
corresponding to the evolution of universe, since a redshift ![]() is in favour of CDM plus a cosmological constant contribution
is in favour of CDM plus a cosmological constant contribution
![]() .
.
From the point of view of quantum field theory it is very hard to explain
why the vacuum energy should have a value of the order of Eq.(7) which,
using the Appendix, can be rewritten as
| (35) |
In fact, since if SUSY were exact, the vacuum energy should be zero, one
might expect that ![]() would depend on the scale of SUSY breaking,
would depend on the scale of SUSY breaking,
![]() ,
,
![]() , i.e., an estimation wrong by 60 orders of
magnitude!
, i.e., an estimation wrong by 60 orders of
magnitude!
One may prefer to think that for some unexplained reason Einstein
cosmological constant and vacuum energy exactly compensates and that what
one observes today is a sort of dynamical cosmological constant due to a
uniform field(15) ![]() called ''quintessence''. Things would go in the
following way:
called ''quintessence''. Things would go in the
following way:
Since the energy-momentum tensor for a scalar field is
| (36) |
| (37) |
On the other hand, the equation of motion, similar to that of axion Eq.(30),
is
| (38) |
Therefore, as discussed for the axion, when ![]() , friction dominates,
, friction dominates, ![]() is constant and from Eq.(37)
is constant and from Eq.(37) ![]() as for a cosmological
constant. The difference is that the rolling down would occur in the present
age because
as for a cosmological
constant. The difference is that the rolling down would occur in the present
age because
| (39) |
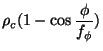 |
(40) | ||
An explanation of why ![]() has this particular value, may be that
has this particular value, may be that ![]() gets its mass through the mixing with pion, as for axion, but with an
interaction between the superheavy fermion and ordinary quarks of
gravitational order instead of strong one(16).
gets its mass through the mixing with pion, as for axion, but with an
interaction between the superheavy fermion and ordinary quarks of
gravitational order instead of strong one(16).
In conclusion, the components of the energy of universe seem reasonably determined, but the identification of their nature requires still a great astrophysical and theoretical effort beyond the standard model of fundamental interactions.