


Next: Scenarios for SUSY Breaking
Up: SUPERSTRING PHENOMENOLOGY AND THE
Previous: Gaugino Condensation
It was found many years ago that some terms can be added
to a supersymmetric lagrangian that do not respect
supersymmetry but still keep the soft ultraviolet
behaviour of the theory. These are the soft-breaking terms. They
are naturally generated after supersymmetry breaking in general
supergravity models and correspond to the following terms
- (i) Scalar masses, implying that the scalars such as squarks,
become usually heavier than the fermions of the same multiplet.
These are terms in the Lagrangian of the form
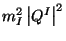 .
.
- (ii) Gaugino masses
 splitting the gauge
multiplets.
splitting the gauge
multiplets.
- (iii)Cubic
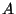 terms. Cubic scalar terms in the potential related
to Yukawa couplings and controlled by arbitrary dimensionfull
coefficients (
terms. Cubic scalar terms in the potential related
to Yukawa couplings and controlled by arbitrary dimensionfull
coefficients (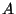 ) of order the gravitino mass.
) of order the gravitino mass.
- (iv)The
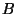 -term. A quadratic term in the potential for the scalars
of the form
-term. A quadratic term in the potential for the scalars
of the form
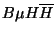 where
where
 represent the Higgs fields and
represent the Higgs fields and
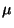 is a constant that gives rise to a term in the original
superpotential
is a constant that gives rise to a term in the original
superpotential
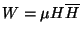 which is allowed by all the
symmetries of the minimal supersymmetric standard model.
Since
which is allowed by all the
symmetries of the minimal supersymmetric standard model.
Since 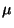 is a dimensionfull parameter it causes a problem to introduce it
in the supersymmetric Lagrangian since it has to be of the order of
the gravitino mass and there is no reason that a term in the
supersymmetric lagrangian knows the scale of the breaking of
supersymmetry.This is known as the
is a dimensionfull parameter it causes a problem to introduce it
in the supersymmetric Lagrangian since it has to be of the order of
the gravitino mass and there is no reason that a term in the
supersymmetric lagrangian knows the scale of the breaking of
supersymmetry.This is known as the 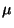 problem and several
solutions have been proposed. Depending on the proposed solution there is
an expression for the parameter
problem and several
solutions have been proposed. Depending on the proposed solution there is
an expression for the parameter 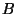 after supersymmetry breaking.
In particular, if
after supersymmetry breaking.
In particular, if 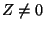 in eq. (21), it can be seen that
the
in eq. (21), it can be seen that
the 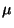 term is generated after supersymmetry breaking. Some calculations
have shown that there are models for which
term is generated after supersymmetry breaking. Some calculations
have shown that there are models for which 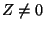 (for recent discussions see [45,95] ).
(for recent discussions see [45,95] ).
In this section we will follow the following strategy.
Treat the supersymmetry breaking mechanism as a black box,
but based on the experience with gaugino condensation,
use that the end result of this mechanism is to induce nonvanishing
values to the auxiliary fields of the moduli or dilaton fields.
Therefore we can parametrize our ignorance of the
particular breaking mechanism by working with general values of these auxiliary fields. Let us for simplicity treat a single modulus field
 and the dilaton
and the dilaton 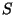 . But the analysis has been done in more general
cases [96,60,97,98]. We can then write the goldstino field (Goldstone fermion
eaten by the gravitino in the process of supersymmetry breaking) as a linear combination of the fermionic components of
. But the analysis has been done in more general
cases [96,60,97,98]. We can then write the goldstino field (Goldstone fermion
eaten by the gravitino in the process of supersymmetry breaking) as a linear combination of the fermionic components of 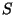 and
and  [98]:
[98]:
 |
(44) |
where the goldstino angle 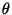 mixing
mixing 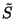 and
and 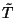 describes the relative contribution of
describes the relative contribution of
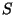 and
and  to the breaking of supersymmetry.
The general procedure for extracting the soft breaking terms is clear.
We start with the supersymmetric lagrangian and substitute in it the nonvanishing auxiliary fields
(
to the breaking of supersymmetry.
The general procedure for extracting the soft breaking terms is clear.
We start with the supersymmetric lagrangian and substitute in it the nonvanishing auxiliary fields
(
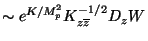 ), using expression (44). Performing the so called flat space limit in which
), using expression (44). Performing the so called flat space limit in which
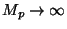 with fixed gravitino mass
with fixed gravitino mass 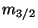 (representing the nonvanishing vev's of the auxiliary fields and parametrizing the breaking of supersymmetry.
We end up with the following values for the soft breaking parameters
[98]:
(representing the nonvanishing vev's of the auxiliary fields and parametrizing the breaking of supersymmetry.
We end up with the following values for the soft breaking parameters
[98]:
From this we can extract several conclusions. The dilaton dominated scenario
for which  , the soft breaking parameters are
universal! This is a very appealing result explaining one of the
less justified assumptions of the minimal supersymmetric standard model.
On the other hand, this scenario is so restrictive that it is
relatively easy to rule it out. Something that was claimed recently
after comparison with the value of the top quark mass, using a particular solution of the
, the soft breaking parameters are
universal! This is a very appealing result explaining one of the
less justified assumptions of the minimal supersymmetric standard model.
On the other hand, this scenario is so restrictive that it is
relatively easy to rule it out. Something that was claimed recently
after comparison with the value of the top quark mass, using a particular solution of the
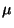 problem above (see for instance
[95] for a recent discussion). The importance of this scenario is that
eqs (45) for
problem above (see for instance
[95] for a recent discussion). The importance of this scenario is that
eqs (45) for  are valid in general and not only for
orbifold models.
For arbitrary mixing angle, the soft breaking terms are not
necessarily universal (unless special values of the modular weights
are taken). In that case we have to confront problems with flavour changing neutral currents [98].
Another conclusion we can extract from the form of the soft breaking terms is that
for negative modular weights, we can get tachyons in the spectrum,
for certain values of the mixing angle. The same condition that avoids tachyons, implies that the gaugino masses have to be bigger than
the scalar masses, unless both vanish; in that case loop corrections may be important to determine the relative masses.
are valid in general and not only for
orbifold models.
For arbitrary mixing angle, the soft breaking terms are not
necessarily universal (unless special values of the modular weights
are taken). In that case we have to confront problems with flavour changing neutral currents [98].
Another conclusion we can extract from the form of the soft breaking terms is that
for negative modular weights, we can get tachyons in the spectrum,
for certain values of the mixing angle. The same condition that avoids tachyons, implies that the gaugino masses have to be bigger than
the scalar masses, unless both vanish; in that case loop corrections may be important to determine the relative masses.
Subsections



Next: Scenarios for SUSY Breaking
Up: SUPERSTRING PHENOMENOLOGY AND THE
Previous: Gaugino Condensation
root
2001-01-22
![]() and the dilaton
and the dilaton ![]() . But the analysis has been done in more general
cases [96,60,97,98]. We can then write the goldstino field (Goldstone fermion
eaten by the gravitino in the process of supersymmetry breaking) as a linear combination of the fermionic components of
. But the analysis has been done in more general
cases [96,60,97,98]. We can then write the goldstino field (Goldstone fermion
eaten by the gravitino in the process of supersymmetry breaking) as a linear combination of the fermionic components of ![]() and
and ![]() [98]:
[98]: