


Next: The Brane-World
Up: SUPERSTRING PHENOMENOLOGY AND THE
Previous: Scenarios for SUSY Breaking
The recent progress in understanding nonperturbative issues of string theory
[10],
[54] has necessarily strong impact on the phenomenological questions,
we are only starting to explore these implications which can be
sumarized as follows.
- (i)
 Unification of theories:
We mentioned in the introduction that there are five consistent superstring theories and each has thousands or millions of different vacua.
It is now believed that the five string theories are related by
strong-weak coupling dualities and furthermore, they appear
to be different limits of a single underlying fundamental theory,
probably in 11D, the
Unification of theories:
We mentioned in the introduction that there are five consistent superstring theories and each has thousands or millions of different vacua.
It is now believed that the five string theories are related by
strong-weak coupling dualities and furthermore, they appear
to be different limits of a single underlying fundamental theory,
probably in 11D, the 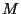 theory
(probably related with membranes or higher dimensional objects such as five-branes),
which is yet to be constructed.
If this is true it may solve the arbitrariness in the number
of fundamental string theories by deriving them from a single
theory.
theory
(probably related with membranes or higher dimensional objects such as five-branes),
which is yet to be constructed.
If this is true it may solve the arbitrariness in the number
of fundamental string theories by deriving them from a single
theory.
- (ii)
 Unification of vacua (?): Recent work
based on comparison of string compactifications with the Seiberg-Witten
theory, has lead to the conclusion that many and probably all
Calabi-Yau compactifications are connected. Then it seems
that not only the five different theories are unified, but also
all the vacua of these theories could
also be unified: since, if they are all connected, we can foresee a
mechanism that lifts the
degeneracy and select one point in the web
of compactifications, something it could not have been done before
because they were thought to be disconnected vacua.
These transitions occur in singular points of the
corresponding moduli space where a particular state
(massless black hole) or even an infinite tower of states (tensionless strings) become massless.
They were partially understood for
Unification of vacua (?): Recent work
based on comparison of string compactifications with the Seiberg-Witten
theory, has lead to the conclusion that many and probably all
Calabi-Yau compactifications are connected. Then it seems
that not only the five different theories are unified, but also
all the vacua of these theories could
also be unified: since, if they are all connected, we can foresee a
mechanism that lifts the
degeneracy and select one point in the web
of compactifications, something it could not have been done before
because they were thought to be disconnected vacua.
These transitions occur in singular points of the
corresponding moduli space where a particular state
(massless black hole) or even an infinite tower of states (tensionless strings) become massless.
They were partially understood for 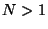 compactifications,
but recently extensions to the phenomenologically interesting
compactifications,
but recently extensions to the phenomenologically interesting
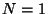 case have been found
[105], implying for instance that models with different
number of families would belong to the same moduli space reducing in some sense the
discrete degeneracy problem to the level of the continuous degeneracy problem
and so we may expect that probably
one particular number of families could
eventually be selected dynamically.
case have been found
[105], implying for instance that models with different
number of families would belong to the same moduli space reducing in some sense the
discrete degeneracy problem to the level of the continuous degeneracy problem
and so we may expect that probably
one particular number of families could
eventually be selected dynamically.
- (iii)Nonperturbative vacua:
The fact that the strong coupling regime of a given string theory
would simply be the weak coupling regime of another string theory
would be very dissapointing since that means that the problems present at
weak coupling would remain at strong coupling.
Fortunately this is not the case. For instance, the strong coupling limit of
the
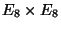 string is believed to be given by
string is believed to be given by 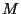 theory compactified in
the orbifold
theory compactified in
the orbifold
 which is just a one dimensional interval.
which is just a one dimensional interval.
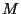 theory contains elementary membranes and their magnetic dual,
theory contains elementary membranes and their magnetic dual,
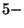 branes. The membranes can end at each of the two
branes. The membranes can end at each of the two  ends
of the interval (fixed points) which are
ends
of the interval (fixed points) which are 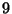 -branes and
generate an
-branes and
generate an 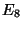 symmetry at each end. The distance between the two
symmetry at each end. The distance between the two
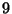 -branes
-branes 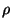 is proportional to the heterotic coupling
and when this is very small the two
is proportional to the heterotic coupling
and when this is very small the two 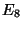 's collapse to a single
's collapse to a single
 point which is the heterotic string. For any finite coupling
the membrane is a cylinder between the two
point which is the heterotic string. For any finite coupling
the membrane is a cylinder between the two 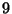 -branes with
heterotic strings at the intersection. This reproduces the standard
perturbative spectrum of heterotic strings.
The new ingredient comes mostly from the
-branes with
heterotic strings at the intersection. This reproduces the standard
perturbative spectrum of heterotic strings.
The new ingredient comes mostly from the 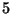 -branes which
for the
-branes which
for the 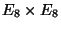 case, carry two-index antisymmetric tensors,
therefore introducing more than one of these fields in the spectrum
after compactifications (in the
case, carry two-index antisymmetric tensors,
therefore introducing more than one of these fields in the spectrum
after compactifications (in the 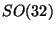 version they may lead to extra vector
fields depending on the compactification).
In perturbative heterotic string there was a single antisymmetric tensor
version they may lead to extra vector
fields depending on the compactification).
In perturbative heterotic string there was a single antisymmetric tensor
 that we saw is dual to an axion field.
The appearance of several of those fields in the spectrum shows clearly that the corresponding vacuum is nonperturbative and may
eventually create more possibilities for using these axion fields
for solving the strong CP problem in string theory.
There is even a model with zero tensor fields. This may be relevant because
that we saw is dual to an axion field.
The appearance of several of those fields in the spectrum shows clearly that the corresponding vacuum is nonperturbative and may
eventually create more possibilities for using these axion fields
for solving the strong CP problem in string theory.
There is even a model with zero tensor fields. This may be relevant because
 is a supersymmetric partner of the dilaton and
having a model without antisymmetric tensors would mean that somehow the dilaton was fixed, lifting the corresponding degeneracy, and acquired a mass
(avoiding the cosmological moduli problem)!
Furthermore for compact spaces with nontrivial
is a supersymmetric partner of the dilaton and
having a model without antisymmetric tensors would mean that somehow the dilaton was fixed, lifting the corresponding degeneracy, and acquired a mass
(avoiding the cosmological moduli problem)!
Furthermore for compact spaces with nontrivial 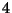 -cycles, the
corresponding
-cycles, the
corresponding 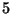 -branes could wrap around those cycles
giving rise to another string (different of course from the one obtained
from the membrane). These nonperturbative strings will generically have their own nonperturbative gauge group, therefore enhancing the maximum rank required in perturbation theory
[55] (the world record seems to be right now a group of rank of order
-branes could wrap around those cycles
giving rise to another string (different of course from the one obtained
from the membrane). These nonperturbative strings will generically have their own nonperturbative gauge group, therefore enhancing the maximum rank required in perturbation theory
[55] (the world record seems to be right now a group of rank of order
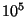 !
[106]).
The physical relevance of the nonperturbative gauge fields is yet to be explored.
!
[106]).
The physical relevance of the nonperturbative gauge fields is yet to be explored.
- (iv)
 Scales in M theory: It is interesting to analyze the different scales present in a
Scales in M theory: It is interesting to analyze the different scales present in a 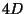 model built from
model built from 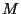 -theory.
There are three relevant scales: the
-theory.
There are three relevant scales: the 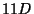 Planck scale
Planck scale 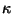 ,
the length of the interval
,
the length of the interval 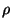 and the overall volume of the
compactified
and the overall volume of the
compactified 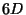 space
space 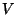 . In the
. In the 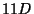 theory, the gauge and gravitational couplings
can be written as:
theory, the gauge and gravitational couplings
can be written as:
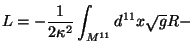 |
|
|
|
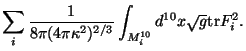 |
|
|
(46) |
Where  is the
is the 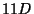 space (bulk) and
space (bulk) and 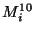 ,
,  are
the two
are
the two 
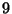 -branes at each end of the interval.
We can see that after compactification, the
-branes at each end of the interval.
We can see that after compactification, the 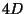 Newton constant
and gauge couplings are given by
Newton constant
and gauge couplings are given by
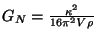 and
and
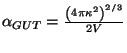 . Notice that now
. Notice that now
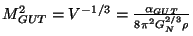 , since we have an extra parameter,
, since we have an extra parameter, 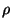 , we can get
, we can get
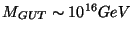 by setting
by setting
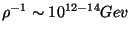 something we could not have done in perturbative heterotic strings.
This has been used by Witten to claim that it may be possible to solve the string unification problem
by tunning the extra parameter as in standard GUTs [107].
We then get the following picture: at large distances the universe looks
something we could not have done in perturbative heterotic strings.
This has been used by Witten to claim that it may be possible to solve the string unification problem
by tunning the extra parameter as in standard GUTs [107].
We then get the following picture: at large distances the universe looks 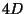 at energy scales between
at energy scales between
 and
and 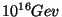 it looks
it looks 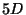 and
at higher scales (smaller distances) it looks
and
at higher scales (smaller distances) it looks 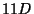 .
This new intermediate scale (
.
This new intermediate scale (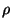 ) may play an interesting role for other
phenomenological and cosmological questions. There is a complication that
for
) may play an interesting role for other
phenomenological and cosmological questions. There is a complication that
for
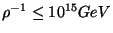 the gauge coupling of one of the gauge groups
blows up, this has been argued by Witten that could put a bound on
Newton's constant on a generic model. There are some specific models which
avoid this problem which makes them more attractive.
Also, the
process of gaugino condensation can be reanalyzed in this picture
[108].
A single condensate in the hidden
the gauge coupling of one of the gauge groups
blows up, this has been argued by Witten that could put a bound on
Newton's constant on a generic model. There are some specific models which
avoid this problem which makes them more attractive.
Also, the
process of gaugino condensation can be reanalyzed in this picture
[108].
A single condensate in the hidden 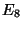
 -brane, does not break supersymmetry in its vecinity nor in the
-brane, does not break supersymmetry in its vecinity nor in the  bulk but due to a topological obstruction it can break
supersymmetry in the observable sector [108]. Note that in this picture the standard model lives at one of the `end of the world' branes while gravity and the moduli fields live in the
bulk but due to a topological obstruction it can break
supersymmetry in the observable sector [108]. Note that in this picture the standard model lives at one of the `end of the world' branes while gravity and the moduli fields live in the 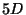 bulk. The possible physical consequences of this new picture are only starting to be
explored [111] (see next section).
bulk. The possible physical consequences of this new picture are only starting to be
explored [111] (see next section).
- (v)
 Nonperturbative superpotential:
It is quite remarkable that recently Witten and others have been able to extract information about superpotentials derived from stringy nonperturbative effects
[109]. At the moment there have been found three classes
of results, depending on the compactification:
Nonperturbative superpotential:
It is quite remarkable that recently Witten and others have been able to extract information about superpotentials derived from stringy nonperturbative effects
[109]. At the moment there have been found three classes
of results, depending on the compactification: 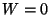 ,
,
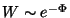 ,
, 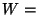 a modular form. Here
a modular form. Here 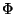 is one of the moduli fields.
The first case is interesting because it means there are compactifications for
which the nonperturbative superpotential vanishes so the only source of
superpotential could be strong coupling infrared effects such as gaugino
condensation making the field theoretical discussion above more
relevant. The second case gives the standard runaway behaviour of the scalar potential and the third possibility is a realization of the kind of duality invariant potentials proposed in the past
[37],[10], in this case there are nontrivial minima and it
is yet to be studied in detail whether supersymmetry could be broken,
in particular these models seem suitable for a realization of the two steps
scenario alluded to before. We hope more progress will be made in this direction
which is addressing the main problem of superstring phenomenology
from a nonperturbative formulation.
is one of the moduli fields.
The first case is interesting because it means there are compactifications for
which the nonperturbative superpotential vanishes so the only source of
superpotential could be strong coupling infrared effects such as gaugino
condensation making the field theoretical discussion above more
relevant. The second case gives the standard runaway behaviour of the scalar potential and the third possibility is a realization of the kind of duality invariant potentials proposed in the past
[37],[10], in this case there are nontrivial minima and it
is yet to be studied in detail whether supersymmetry could be broken,
in particular these models seem suitable for a realization of the two steps
scenario alluded to before. We hope more progress will be made in this direction
which is addressing the main problem of superstring phenomenology
from a nonperturbative formulation.
- (vi)Stringy
 effects: Some time ago, Shenker proposed that in string theory,
there would appear nonperturbative effects of the form
effects: Some time ago, Shenker proposed that in string theory,
there would appear nonperturbative effects of the form  on top of the standard field theoretical effects of the form
on top of the standard field theoretical effects of the form 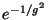 . These have been
argued to correct the Kähler potential and contribute to the dilaton potential in such a way that the dilaton can be fixed even with a single exponential in
. These have been
argued to correct the Kähler potential and contribute to the dilaton potential in such a way that the dilaton can be fixed even with a single exponential in  [58]. Recently, these effects were explicitly computed for the heterotic string for a particular compactification [110].
[58]. Recently, these effects were explicitly computed for the heterotic string for a particular compactification [110].
We can see that many of the results from string perturbation theory are modified
by the nonperturbative information obtained so far. Some of the other results
are expected to be modified or need revision, for instance the nonexistence of
global symmetries
was proved using CFT techniques which are explicitly perturbative, it is expected that being string theory a theory of gravity, global symmetries will not be allowed
(as usually found studying black holes and wormholes), but a general nonpertubative proof
is not available yet. Also, the main problems such as supersymmetry breaking,
are still open which is a good motivation to work on this field.
Now we turn to probably the most striking result of the second string
revolution, namely the possibility that we live on a hypersurface
inside a higher dimensional spacetime.



Next: The Brane-World
Up: SUPERSTRING PHENOMENOLOGY AND THE
Previous: Scenarios for SUSY Breaking
root
2001-01-22
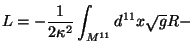
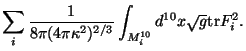
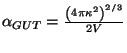 . Notice that now
. Notice that now
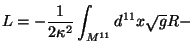
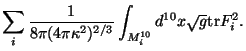
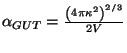 . Notice that now
. Notice that now