


Next: Realistic Type I,II Brane
Up: The Brane-World
Previous: The Brane-World
It is important to realise the difference between the brane world and
the better known Kaluza-Klein scenario. In Kaluza-Klein all fields
feel the extra dimensions whereas in the brane world, only a subset of
the fields (gravity and moduli fields in string theory) feel all the
extra dimensions.
This simple fact has very important physical implications regarding
the possible values of the fundamental scale. An explicit way to see
the difference is comparing the low-energy effective actions for
perturbative heterotic strings and type I strings. In the heterotic
case, both gravity and the gauge fields live on the full
10-dimensional spacetime corresponding to a standard Kaluza-Klein
scenario. The low-energy effective action in 10 dimensions takes the
form:
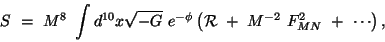 |
(47) |
where
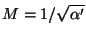 is the string scale and
is the string scale and 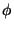 is
the dilaton field.
Upon compactification to 4-dimensions each of the two terms in the
action above will get a volume factor coming from the integration of
the 6 extra dimensions. This gives us an expression for the
gravitational and gauge couplings (the numerical coefficients of each
of the two terms above) of the form:
is
the dilaton field.
Upon compactification to 4-dimensions each of the two terms in the
action above will get a volume factor coming from the integration of
the 6 extra dimensions. This gives us an expression for the
gravitational and gauge couplings (the numerical coefficients of each
of the two terms above) of the form:
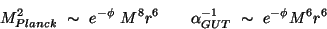 |
(48) |
where 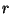 is the overall size of the extra dimensions.
Taking the ratio of those expressions the volume factors cancel
and we get
is the overall size of the extra dimensions.
Taking the ratio of those expressions the volume factors cancel
and we get
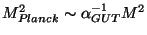 . Therefore for
. Therefore for
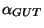 not much different from 1 (as expected) we have to have
the fundamental scale
not much different from 1 (as expected) we have to have
the fundamental scale 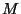 to be of the same order of magnitude as the
gravitational scale
to be of the same order of magnitude as the
gravitational scale
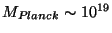 GeV. This was the old
belief that the string scale was the Planck scale.
Things are very different in the brane world scenario as we can see
for the case of the type I string.
For a configuration with the standard model spectrum belonging to
a Dp-brane, the low energy action in 4-dimensions takes the form:
GeV. This was the old
belief that the string scale was the Planck scale.
Things are very different in the brane world scenario as we can see
for the case of the type I string.
For a configuration with the standard model spectrum belonging to
a Dp-brane, the low energy action in 4-dimensions takes the form:
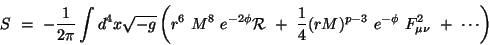 |
(49) |
Comparing the coefficient of the Einstein term with the physical
Planck mass 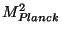 and the coefficient of the gauge kinetic
term with the physical gauge coupling constant
and the coefficient of the gauge kinetic
term with the physical gauge coupling constant 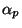 (
(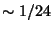 at the string scale), we find the relation:
at the string scale), we find the relation:
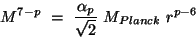 |
(50) |
from which we can easily see that if the Standard Model
fits inside a D3-brane, for instance,
we may have 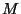 substantially smaller than
substantially smaller than
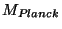 as long as the sizes of the extra dimensions are large enough.
Given the fact that we do not have a way to fix the size of the extra
dimensions we can take advantage of our ignorance
and follow a bottom-up approach considering different
possibilities motivated by phenomenological inputs.
Several scenarios have been proposed depending on the value of the
fundamental scale. The four main scenarios at present correspond to
as long as the sizes of the extra dimensions are large enough.
Given the fact that we do not have a way to fix the size of the extra
dimensions we can take advantage of our ignorance
and follow a bottom-up approach considering different
possibilities motivated by phenomenological inputs.
Several scenarios have been proposed depending on the value of the
fundamental scale. The four main scenarios at present correspond to
-
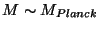 . This is just the old perturbative heterotic
string case
corresponding to compactification scale close to the Planck scale.
There is nothing wrong with this possibility.
Research over the years has shown
difficult to obtain gauge coupling unification in this case.
. This is just the old perturbative heterotic
string case
corresponding to compactification scale close to the Planck scale.
There is nothing wrong with this possibility.
Research over the years has shown
difficult to obtain gauge coupling unification in this case.
-
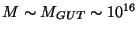 GeV. Obtained for
GeV. Obtained for
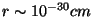 in the expression above. This proposal [111] was
made precisely to `solve' the gauge coupling unification problem in
string theories. This requires a compactification scale of order
in the expression above. This proposal [111] was
made precisely to `solve' the gauge coupling unification problem in
string theories. This requires a compactification scale of order
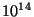 GeV.
Recent progress has been made [42] in looking for three
generation models realising this
scenario from the Horava-Witten construction
but, so far, not from
type I models.
GeV.
Recent progress has been made [42] in looking for three
generation models realising this
scenario from the Horava-Witten construction
but, so far, not from
type I models.
-
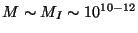 GeV. If the world is a D3-brane we
can see that this scale is obtained from the equations above for
GeV. If the world is a D3-brane we
can see that this scale is obtained from the equations above for
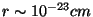 . This proposal
[112], was based on the special role played by the
intermediate scale
. This proposal
[112], was based on the special role played by the
intermediate scale 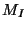 in different ideas beyond he standard model.
Particularly the scale of supersymmetry breaking in gravity mediated
supersymmetry breaking scenario. This then allows to identify the
string scale with the supersymmetry breaking scale and opens up the
room for non supersymmetric string models to be relevant at
low-energies. Explicit models realising this scenario will be discussed
in the next section.
in different ideas beyond he standard model.
Particularly the scale of supersymmetry breaking in gravity mediated
supersymmetry breaking scenario. This then allows to identify the
string scale with the supersymmetry breaking scale and opens up the
room for non supersymmetric string models to be relevant at
low-energies. Explicit models realising this scenario will be discussed
in the next section.
-
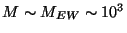 GeV. This is obtained for overall
radius
GeV. This is obtained for overall
radius
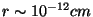 above and if only two of the six dimensions
were large this would have given us the famous
above and if only two of the six dimensions
were large this would have given us the famous 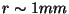 quoted as
the extreme case of the brane world scenario
since lengths bigger than this
would have been observed by deviations of gravity.
This is the most popular scenario [113]
due to its proximity with experiment. It has opened up a completely
new approach towards looking for physics beyond the standard model
at present and future experiments, especially after the work of
Arkani-Hamed, Dimopoulos and Dvali [114]
where a detailed analysis was done
about the possible experimental, astrophysical and cosmological
constraints of this scenario which range from comparisons with Van der
Waals forces in molecules to overcooling of supernovae, especially
supernova 1987a.
Concrete string models realising
this scenario do not exist. We will discuss some
attempts in the next section.
quoted as
the extreme case of the brane world scenario
since lengths bigger than this
would have been observed by deviations of gravity.
This is the most popular scenario [113]
due to its proximity with experiment. It has opened up a completely
new approach towards looking for physics beyond the standard model
at present and future experiments, especially after the work of
Arkani-Hamed, Dimopoulos and Dvali [114]
where a detailed analysis was done
about the possible experimental, astrophysical and cosmological
constraints of this scenario which range from comparisons with Van der
Waals forces in molecules to overcooling of supernovae, especially
supernova 1987a.
Concrete string models realising
this scenario do not exist. We will discuss some
attempts in the next section.
Notice that only the first scenario was possible following the
standard Kaluza-Klein approach in the perturbative heterotic string
models.
The brane world opened up the possibility of the next three
scenarios as well as any other scale in the range
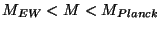 .
.



Next: Realistic Type I,II Brane
Up: The Brane-World
Previous: The Brane-World
root
2001-01-22