


Next: Interacting Strings and the
Up: Perturbative String and Superstring
Previous: Perturbative String and Superstring
Closed Strings
The spectrum of the closed string can be obtained from the combination of the left-moving
states and the right-moving ones. The ground state (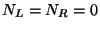 ) is given by
) is given by
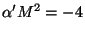 . That means that the ground state includes a tachyon. The first
excited state (
. That means that the ground state includes a tachyon. The first
excited state ( ) is massless and it is given by
) is massless and it is given by
 . This state can be naturally
decomposed into irreducible representations of the little group
. This state can be naturally
decomposed into irreducible representations of the little group  as follows
as follows
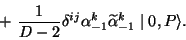 |
(9) |
The first term of the rhs is interpreted as a spin 2 massless particle
 (graviton). The second term is a range 2 anti-symmetric tensor
(graviton). The second term is a range 2 anti-symmetric tensor
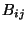 . While the last term is an scalar field
. While the last term is an scalar field
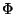 (dilaton). Higher excited massive states are combinations of
irreducible representations of the corresponding little group SO
(dilaton). Higher excited massive states are combinations of
irreducible representations of the corresponding little group SO truecm
Open Strings
For the open string, the ground state includes once again a tachyon since
truecm
Open Strings
For the open string, the ground state includes once again a tachyon since
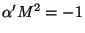 . The first exited state
. The first exited state
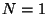 is given by a massless vector field in 26 dimensions. The second excitation level
is given by the massive states
is given by a massless vector field in 26 dimensions. The second excitation level
is given by the massive states
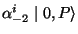 and
and
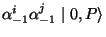 which are in irreducible
representations of the little group SO
which are in irreducible
representations of the little group SO .
truecm
.
truecm



Next: Interacting Strings and the
Up: Perturbative String and Superstring
Previous: Perturbative String and Superstring
root
2001-01-15