


Next: The evolution of baryonic
Up: THE LARGE-SCALE STRUCTURE OF
Previous: The Zeldovich approximation
In the description of the evolution of density inhomogeneities, one
often make the simplifying assumption that the initial power-spectrum
has the simple power-law expression
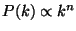 . Although the
scale-free Zeldovich spectrum,
. Although the
scale-free Zeldovich spectrum,  , is expected on the
grounds of the classical inflationary scenario, nevertheless
distortions of its shape should arise during the subsequent phases of
cosmic expansion, and characteristic scales are imprinted on the form
of
, is expected on the
grounds of the classical inflationary scenario, nevertheless
distortions of its shape should arise during the subsequent phases of
cosmic expansion, and characteristic scales are imprinted on the form
of 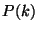 at the onset of the structure formation. Since the amount
of such distortions and the scales at which they occur are strictly
related to the nature of the fluctuations and to the matter content of
the Universe, their knowledge becomes of crucial relevance in order to
fix the initial conditions for the galaxy formation process.
at the onset of the structure formation. Since the amount
of such distortions and the scales at which they occur are strictly
related to the nature of the fluctuations and to the matter content of
the Universe, their knowledge becomes of crucial relevance in order to
fix the initial conditions for the galaxy formation process.
Theoretical models for the determination of the power-spectrum, which is
responsible for structure formation, starts from the assumption of a
primordial  at a sufficiently high redshift,
at a sufficiently high redshift,
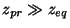 [
[
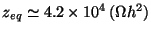 is the redshift of the epoch
of matter-radiation equality]. The usual choice
is the redshift of the epoch
of matter-radiation equality]. The usual choice 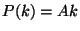 corresponds to
the Harrison-Zeldovich spectrum. Due to the evolution of density
perturbations, the slope of the power-spectrum is left unchanged at
wavelengths
corresponds to
the Harrison-Zeldovich spectrum. Due to the evolution of density
perturbations, the slope of the power-spectrum is left unchanged at
wavelengths
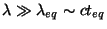 , that exceed the horizon
size at
, that exceed the horizon
size at 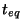 . On the contrary, the shape of the spectrum at
. On the contrary, the shape of the spectrum at
 crucially depends on the nature of the matter which
dominates the expansion. In order to account for these effects, the
post-recombination spectrum is usually written as
crucially depends on the nature of the matter which
dominates the expansion. In order to account for these effects, the
post-recombination spectrum is usually written as
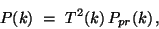 |
(21) |
where the transfer function 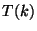 conveys all the informations
about the pre-recombination evolution and the nature of the matter content.
conveys all the informations
about the pre-recombination evolution and the nature of the matter content.
Subsections



Next: The evolution of baryonic
Up: THE LARGE-SCALE STRUCTURE OF
Previous: The Zeldovich approximation
Waleska Aldana Segura
2001-01-16
![]() at a sufficiently high redshift,
at a sufficiently high redshift,
![]() [
[
![]() is the redshift of the epoch
of matter-radiation equality]. The usual choice
is the redshift of the epoch
of matter-radiation equality]. The usual choice ![]() corresponds to
the Harrison-Zeldovich spectrum. Due to the evolution of density
perturbations, the slope of the power-spectrum is left unchanged at
wavelengths
corresponds to
the Harrison-Zeldovich spectrum. Due to the evolution of density
perturbations, the slope of the power-spectrum is left unchanged at
wavelengths
![]() , that exceed the horizon
size at
, that exceed the horizon
size at ![]() . On the contrary, the shape of the spectrum at
. On the contrary, the shape of the spectrum at
![]() crucially depends on the nature of the matter which
dominates the expansion. In order to account for these effects, the
post-recombination spectrum is usually written as
crucially depends on the nature of the matter which
dominates the expansion. In order to account for these effects, the
post-recombination spectrum is usually written as