


Next: The spectrum of primordial
Up: Describing the inhomogeneities of
Previous: The linear approximation
A simple and elegant approximation to describe the non-linear stage of
gravitational evolution has been developed by Zeldovich [38]
(see the review by Shandarin & Zeldovich [28], for an
exhaustive description of the Zeldovich approximation). In this
approach, the initial matter distribution is considered to be
homogeneous and collisionless. If the unperturbed (initial) Lagrangian
coordinates of the particles are described by 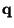 , then the Eulerian
coordinates of the particles at the time
, then the Eulerian
coordinates of the particles at the time  are given by
are given by
![\begin{displaymath}
\mbox{\bf r}(\mbox{\bf q},t) = a(t) [\mbox{\bf q}+b(t) \mbox{\bf s}(\mbox{\bf q})] .
\end{displaymath}](img88.gif) |
(15) |
Here 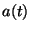 is the cosmic expansion factor and
is the cosmic expansion factor and  the growing rate of
linear fluctuations, as provided by eq.(13). Moreover, the
velocity term
the growing rate of
linear fluctuations, as provided by eq.(13). Moreover, the
velocity term
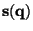 , which provides the particle displacement with
respect to the initial (Laplacian) position, is
related to the potential
, which provides the particle displacement with
respect to the initial (Laplacian) position, is
related to the potential
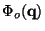 originated by the initially linear
fluctuations, according to
originated by the initially linear
fluctuations, according to
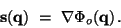 |
(16) |
In order to better visualize the meaning of eq.(15), let us
consider a pressureless and viscosity-free, homogeneous medium without any
gravitational interaction. For this system, the Eulerian positions  of
the particles at time
of
the particles at time  are related to the Lagrangian positions
are related to the Lagrangian positions 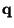 by
the linear relation
by
the linear relation
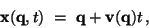 |
(17) |
being
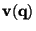 the initial velocity. The above expression is essentially
analogous to the Zeldovich approximation (15), apart from the
presence of the
the initial velocity. The above expression is essentially
analogous to the Zeldovich approximation (15), apart from the
presence of the 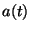 term, which accounts for the background cosmic
expansion, and of the
term, which accounts for the background cosmic
expansion, and of the  term, which accounts for the presence of
gravity, giving a deceleration of particles along the trajectories
(actually,
term, which accounts for the presence of
gravity, giving a deceleration of particles along the trajectories
(actually,
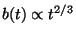 in a
in a 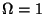 matter dominated
Universe).
matter dominated
Universe).
Since at 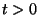 density inhomogeneities are created, mass conservation
requires that
density inhomogeneities are created, mass conservation
requires that
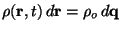 , so that the
density field as a function of Lagrangian coordinates reads
, so that the
density field as a function of Lagrangian coordinates reads
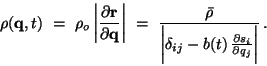 |
(18) |
Here the deformation tensor
 accounts for the
gravitational evolution of the fluid, while
accounts for the
gravitational evolution of the fluid, while
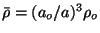 is
the mean density at time
is
the mean density at time  . At the linear stage, when
. At the linear stage, when
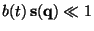 , eq.(18) can be approximated by
, eq.(18) can be approximated by
![\begin{displaymath}
\rho(\mbox{\bf q},t) \simeq \bar \rho [1-b(t){\bf\nabla}_q\cdot \mbox{\bf s}(\mbox{\bf q})] ,
\end{displaymath}](img104.gif) |
(19) |
so that
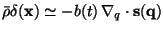 and we recover (the growing mode of) the linear solution.
and we recover (the growing mode of) the linear solution.
More in general, since the expression (16) for
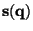 makes the deformation tensor a real symmetric matrix, its eigenvectors
define a set of three principal (orthogonal) axes. After
diagonalization, eq.(18) can be written in terms of its
eigenvalues
makes the deformation tensor a real symmetric matrix, its eigenvectors
define a set of three principal (orthogonal) axes. After
diagonalization, eq.(18) can be written in terms of its
eigenvalues
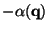 ,
,
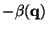 and
and
 , which
give the contraction or expansion along the three principal axes:
, which
give the contraction or expansion along the three principal axes:
![\begin{displaymath}
\rho(\mbox{\bf q},t) = {\bar \rho \over [1-b(t) \alpha(\mbo...
...(t) \beta(\mbox{\bf q})]
[1-b(t) \gamma(\mbox{\bf q})]} .
\end{displaymath}](img109.gif) |
(20) |
If the eigenvalues are ordered in such a way that
 , then, as
, then, as  grows, the first singularity in eq.(20) occurs in
correspondence of the Lagrangian coordinate
grows, the first singularity in eq.(20) occurs in
correspondence of the Lagrangian coordinate
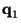 , where
, where 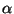 attains its maximum positive value
attains its maximum positive value 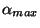 , at the time
, at the time 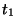 such that
such that
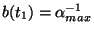 . This corresponds to the
formation of a pancake (sheet-like structure) by contraction along one
of the principal axes. For this reason, Zeldovich [38] argued
that pancakes are the first structures formed by gravitational
clustering. Other structures like filaments and knots come from
simultaneous contractions along two and three axes, respectively.
Doroshkevich [8] evaluated the probability distribution for
the three eigenvalues in the case of a Gaussian random field and
concluded that simultaneous vanishing of more than one of them is
quite unlikely. Thus, in this scenario, pancakes are the dominant
features arising from the first stages of non-linear gravitational
clustering.
. This corresponds to the
formation of a pancake (sheet-like structure) by contraction along one
of the principal axes. For this reason, Zeldovich [38] argued
that pancakes are the first structures formed by gravitational
clustering. Other structures like filaments and knots come from
simultaneous contractions along two and three axes, respectively.
Doroshkevich [8] evaluated the probability distribution for
the three eigenvalues in the case of a Gaussian random field and
concluded that simultaneous vanishing of more than one of them is
quite unlikely. Thus, in this scenario, pancakes are the dominant
features arising from the first stages of non-linear gravitational
clustering.
The Zeldovich approximation predicts the first non-linear structure to
arise in correspondence of the high peaks of the
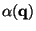 field
and represents a significant step forward with respect to linear
theory and in fact it has been successfully applied to describe the
large scale clustering in the distribution of galaxy clusters.
field
and represents a significant step forward with respect to linear
theory and in fact it has been successfully applied to describe the
large scale clustering in the distribution of galaxy clusters.
However, within the Zeldovich prescription, after a pancake forms in
correspondence of crossing of particle orbits, such particles continue
travelling along straight lines, according to
eq.(15). Viceversa, in the framework of a realistic
description of gravitational dynamics, we expect that the potential
wells, that correspond to non-linear structures, should be able to
retain particles and to accrete from surrounding regions.



Next: The spectrum of primordial
Up: Describing the inhomogeneities of
Previous: The linear approximation
Waleska Aldana Segura
2001-01-16
![]() density inhomogeneities are created, mass conservation
requires that
density inhomogeneities are created, mass conservation
requires that
![]() , so that the
density field as a function of Lagrangian coordinates reads
, so that the
density field as a function of Lagrangian coordinates reads
![]() makes the deformation tensor a real symmetric matrix, its eigenvectors
define a set of three principal (orthogonal) axes. After
diagonalization, eq.(18) can be written in terms of its
eigenvalues
makes the deformation tensor a real symmetric matrix, its eigenvectors
define a set of three principal (orthogonal) axes. After
diagonalization, eq.(18) can be written in terms of its
eigenvalues
![]() ,
,
![]() and
and
![]() , which
give the contraction or expansion along the three principal axes:
, which
give the contraction or expansion along the three principal axes:
![]() field
and represents a significant step forward with respect to linear
theory and in fact it has been successfully applied to describe the
large scale clustering in the distribution of galaxy clusters.
field
and represents a significant step forward with respect to linear
theory and in fact it has been successfully applied to describe the
large scale clustering in the distribution of galaxy clusters.