


Next: Superstrings
Up: Perturbative String and Superstring
Previous: Spectrum of the Bosonic
Interacting Strings
So far we have described the free propagation of a closed (or open) bosonic string. In what
follows we consider the interaction of these strings. Here we focus in the closed string case,
the open case requires from further definitions. The interaction of strings at the perturbative
level is just the extension of the technique of Feynman diagrams for point particles to extended
objets. The vacuum-vacuum amplitude 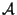 is given by
is given by
![\begin{displaymath}
{\cal A} \sim \int {\cal D} h_{ab} {\cal D} X^I exp \bigg(i S_P[X^I,h_{ab}] \bigg).
\end{displaymath}](img105.gif) |
(10) |
The interacting case requires to sum over all loop diagrams. In the closed string case it means
that we have to sum over all compact orientable surfaces. In two
dimensions these surfaces are
completely characterized by their number of holes  (the genus). The
relevant topological invariant is the Euler number
(the genus). The
relevant topological invariant is the Euler number
 , where
, where  is the scalar curvature of the worldsheet
is the scalar curvature of the worldsheet  . In order to
include the interaction of strings, the generalization of the Polyakov action consistent with
its symmetries is given by
. In order to
include the interaction of strings, the generalization of the Polyakov action consistent with
its symmetries is given by
![\begin{displaymath}
S= S_P[X^I,h_{ab}] + {\Phi(X^I) \over 4 \pi} \int_{\Sigma} d^2 \sigma \sqrt{-h} R^{(2)},
\end{displaymath}](img109.gif) |
(11) |
where 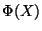 is an scalar background field and represents the
gravitational coupling constant of the two-dimensional Einstein-Hilbert Lagrangian.
is an scalar background field and represents the
gravitational coupling constant of the two-dimensional Einstein-Hilbert Lagrangian.
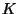 in the above equation stands for the geodesic curvature of
in the above equation stands for the geodesic curvature of  .
If we define the string coupling constant by
.
If we define the string coupling constant by
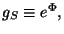 then Eq. (10)
generalizes to
then Eq. (10)
generalizes to
![\begin{displaymath}
{\cal A} \sim \sum_{\chi} g_S^{\chi(\Sigma)} \int {\cal D} h_{ab} {\cal D} X^I
exp \bigg(i S_P[X^I,h_{ab}]
\bigg).
\end{displaymath}](img113.gif) |
(12) |
The amplitude defined on-shell correspond to 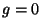 and the rest (
and the rest (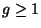 ) corresponds to
) corresponds to
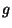 -loop corrections.
The definition of correlation functions of operators requires of the idea of vertex
operators
-loop corrections.
The definition of correlation functions of operators requires of the idea of vertex
operators
 . These operators are defined as
. These operators are defined as
 |
(13) |
where
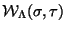 (with
(with 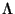 being a generic massless field of the bosonic
spectra) is a local operator assigned
to some specific state of the
spectrum of the theory. For instance for the tachyon it is given by
being a generic massless field of the bosonic
spectra) is a local operator assigned
to some specific state of the
spectrum of the theory. For instance for the tachyon it is given by
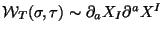 . While that for the graviton
. While that for the graviton 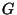 with polarization
with polarization
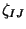 it is given by
it is given by
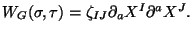 Local operators
Local operators
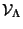 are diffeomorphism and conformal invariant and therefore more convenient
to define scattering amplitudes.
Thus one can define the scattering amplitude of the vertex field operators by
their
corresponding invariant operators
are diffeomorphism and conformal invariant and therefore more convenient
to define scattering amplitudes.
Thus one can define the scattering amplitude of the vertex field operators by
their
corresponding invariant operators
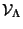 . In perturbation theory the
scattering amplitude is given by
. In perturbation theory the
scattering amplitude is given by
![\begin{displaymath}
{\cal A}(\Lambda_1,k_1; \dots \Lambda_N,k_N) \sim \sum_{\ch...
...[X^I,h_{ab}] \bigg) \prod_{i=1}^N {\cal
V}_{\Lambda_i}(k_i).
\end{displaymath}](img125.gif) |
(14) |
This scattering amplitude is, of course, proportional to the correlation function of the
product of 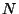 invariant operators
invariant operators
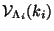 as follows
as follows
 |
(15) |
truecm
Effective String Actions
In order to make contact with the spacetime physics we now describe how the
spacetime equations of motion come from conformal invariance conditions for the
non-linear sigma model in curved spaces. The immediate generalization of the Polyakov
action is
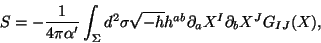 |
(16) |
where 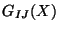 is an arbitrary background metric of the curved target space
is an arbitrary background metric of the curved target space 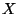 . The
perturbation of this metric
. The
perturbation of this metric
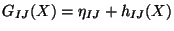 in the partition function
in the partition function
![$Z\sim exp \big(-S[X^I, \eta_{IJ} + h_{IJ}]\big)$](img131.gif) , leads to
an expansion in powers of
, leads to
an expansion in powers of 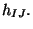 This partition
function can be easily interpreted as that coming from the interaction of the
string with a coherent state of gravitons with invariant operator
This partition
function can be easily interpreted as that coming from the interaction of the
string with a coherent state of gravitons with invariant operator
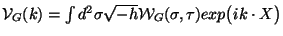 with
with
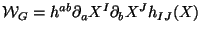 .
On the other hand, the Polyakov action can be generalized to be consistent with
all symmetries and with the massless spectrum of the
bosonic closed strings in the form of a non-linear sigma model
.
On the other hand, the Polyakov action can be generalized to be consistent with
all symmetries and with the massless spectrum of the
bosonic closed strings in the form of a non-linear sigma model
![\begin{displaymath}
\widehat{S}= {1 \over 4 \pi \alpha '} \int_{\Sigma} d^2 \si...
..._a X^{I}
\partial_b X^{J} + \alpha ' \Phi(X) R^{(2)} \bigg],
\end{displaymath}](img135.gif) |
(17) |
where 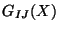 is the target space curved metric,
is the target space curved metric, 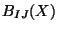 is an
anti-symmetric field, also called the Kalb-Ramond field, and
is an
anti-symmetric field, also called the Kalb-Ramond field, and 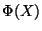 is the scalar
field called the dilaton field. From the viewpoint of the two-dimensional
non-linear sigma model these background fields can be regarded as coupling
constants and the renormalization group techniques become applied. The computation of the
quantum conformal anomaly by using the dimensional regularization method, leads to
express the energy-momentum trace as a linear combination
is the scalar
field called the dilaton field. From the viewpoint of the two-dimensional
non-linear sigma model these background fields can be regarded as coupling
constants and the renormalization group techniques become applied. The computation of the
quantum conformal anomaly by using the dimensional regularization method, leads to
express the energy-momentum trace as a linear combination
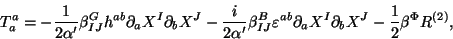 |
(18) |
where 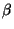 are the one-loop beta functions associated with each coupling
constant or background field. They are explicitly computed and give
are the one-loop beta functions associated with each coupling
constant or background field. They are explicitly computed and give
 |
(19) |
 |
(20) |
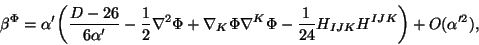 |
(21) |
where
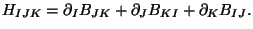 Weyl invariance at the quantum level implies the vanishing of the conformal anomaly
and therefore the vanishing of each beta function. This leads to three coupled
field equations for the background fields. These conditions for these fields can been
regarded as equations of motion derivable from the spacetime action in
Weyl invariance at the quantum level implies the vanishing of the conformal anomaly
and therefore the vanishing of each beta function. This leads to three coupled
field equations for the background fields. These conditions for these fields can been
regarded as equations of motion derivable from the spacetime action in 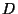 dimensions
dimensions
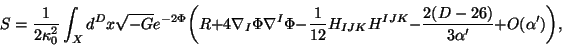 |
(22) |
where  is a normalization constant.
It is interesting to see that a redefinition of background metric under the
transformation in
is a normalization constant.
It is interesting to see that a redefinition of background metric under the
transformation in 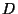 dimensions
dimensions
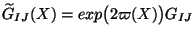 with
with
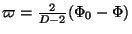 leads to the background action in the
`Einstein frame'
leads to the background action in the
`Einstein frame'
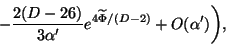 |
(23) |
where
![$\widetilde{R} = e^{-2 \varpi} \big[ R - 2 (D-1) \nabla^2 \varpi -(D-2)(D-1)
\partial_{I} \varpi \partial^{I} \varpi \big]$](img149.gif) and
and
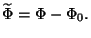 The form of this action will of extreme importance later when we describe the strong/weak
coupling duality in effective supergravity actions of the different superstring theories
types. In the above action
The form of this action will of extreme importance later when we describe the strong/weak
coupling duality in effective supergravity actions of the different superstring theories
types. In the above action
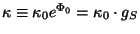 is the
gravitational coupling constant in
is the
gravitational coupling constant in 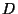 dimensions, i.e.
dimensions, i.e.
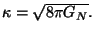 A very close procedure can be performed for the open string and compute its effective low
energy action. It was done about 15 years ago and for gauge fields with constant
field strength
A very close procedure can be performed for the open string and compute its effective low
energy action. It was done about 15 years ago and for gauge fields with constant
field strength 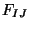 it is given by the Dirac-Born-Infeld action
it is given by the Dirac-Born-Infeld action
 |
(24) |
Later we shall say something about some applications of this effective action.
truecm



Next: Superstrings
Up: Perturbative String and Superstring
Previous: Spectrum of the Bosonic
root
2001-01-15
![\begin{displaymath}
{\cal A} \sim \sum_{\chi} g_S^{\chi(\Sigma)} \int {\cal D} h_{ab} {\cal D} X^I
exp \bigg(i S_P[X^I,h_{ab}]
\bigg).
\end{displaymath}](img113.gif)
![\begin{displaymath}
{\cal A}(\Lambda_1,k_1; \dots \Lambda_N,k_N) \sim \sum_{\ch...
...[X^I,h_{ab}] \bigg) \prod_{i=1}^N {\cal
V}_{\Lambda_i}(k_i).
\end{displaymath}](img125.gif)
