Next: T-duality, D-branes and Brane
Up: Perturbative String and Superstring
Previous: Heterotic Superstrings
In order to connect superstring theories to the observed 4-dimensional spacetime
physics,
we have to reduce the critical dimension 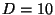 to four dimensions. To preserve
certain supersymmetry consistent with chirality in four dimensions
it is necessary to require some properties to the ten
dimensional spacetime
to four dimensions. To preserve
certain supersymmetry consistent with chirality in four dimensions
it is necessary to require some properties to the ten
dimensional spacetime 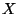 . Perhaps the simplest ansatz is to assume that
the four-dimensional Minkowski spacetime
. Perhaps the simplest ansatz is to assume that
the four-dimensional Minkowski spacetime  and a six-dimensional internal space
and a six-dimensional internal space  factorizes
as
factorizes
as
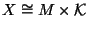 , where
, where  has tiny dimensions and
unobservable in our present experiments. It is worth to say that this factorization ansatz is not
unique and other
possibility is the warped compactification of the celebrated Randall-Sundrum
scenarios, which are nicely reviewed in Ref. [9].
It is useful to classify the compactifications according to how much
supersymmetries
is broken, because this number is related with the quantum corrections that
we shall consider. We choose
has tiny dimensions and
unobservable in our present experiments. It is worth to say that this factorization ansatz is not
unique and other
possibility is the warped compactification of the celebrated Randall-Sundrum
scenarios, which are nicely reviewed in Ref. [9].
It is useful to classify the compactifications according to how much
supersymmetries
is broken, because this number is related with the quantum corrections that
we shall consider. We choose  to be a
manifold with the property that a
certain
number of supersymmetries are preserved3.
We are now looking for conditions in the background which leave some
supersymmetry
unbroken. These conditions are given by null variations of the Fermi fields.
Consider the diagonal metric for ten-dimensional spacetime
to be a
manifold with the property that a
certain
number of supersymmetries are preserved3.
We are now looking for conditions in the background which leave some
supersymmetry
unbroken. These conditions are given by null variations of the Fermi fields.
Consider the diagonal metric for ten-dimensional spacetime 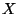 given by
given by
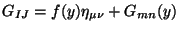 where
where 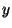 denotes the compactified coordinates and
denotes the compactified coordinates and 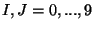 ,
,
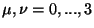 ,
,  . For
. For 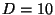 ,
, 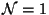 heterotic string theory the Fermi fields
variations are:
heterotic string theory the Fermi fields
variations are:
- gravitino:
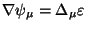 ,
,

- dilatino:
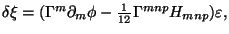
- gaugino:
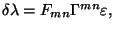
where  is a Weyl-Majorana spinor in ten dimensions,
is a Weyl-Majorana spinor in ten dimensions,
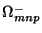 is the
internal component of
is the
internal component of
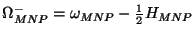 ,
, 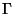 are the
Dirac matrices.
The compactification ansatz
are the
Dirac matrices.
The compactification ansatz
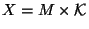 breaks the Lorentz group SO(9,1) into
SO
breaks the Lorentz group SO(9,1) into
SO
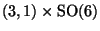 . In the spinor representation 16
the Weyl-Majorana supersymmetry parameter
. In the spinor representation 16
the Weyl-Majorana supersymmetry parameter
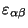 decomposes as
decomposes as
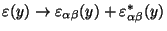 under
under
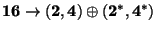 . The general form of
. The general form of
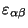 is
is
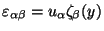 with
with 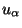 an
arbitrary Weyl spinor. When we put the condition that Fermi fields variations vanish, then
each internal spinor
an
arbitrary Weyl spinor. When we put the condition that Fermi fields variations vanish, then
each internal spinor
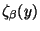 gives the minimal (
gives the minimal (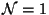 )
)  supersymmetric algebra.
Now, by the null fermi fields variations we can find conditions in the background
fields assuming that
supersymmetric algebra.
Now, by the null fermi fields variations we can find conditions in the background
fields assuming that 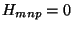 . These are:
The last equation tell us that
. These are:
The last equation tell us that 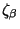 is covariantly
constant on the internal space
is covariantly
constant on the internal space  , and implies that
, and implies that  is Ricci-flat.
This is because
is Ricci-flat.
This is because
![$[\nabla_m,\nabla_n]\zeta =\frac{1}{4}R_{mnpq}\Gamma^{pq}\zeta=0$](img251.gif) . For this
reason, in general
. For this
reason, in general
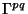 do not belong to SO(6) but to SU(3), which is a subgroup that
leaves one component of the spinor
do not belong to SO(6) but to SU(3), which is a subgroup that
leaves one component of the spinor 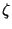 invariant. Thus the
compact
manifold
invariant. Thus the
compact
manifold  must have SU(3) holonomy. The second unbroken susy condition
implies that the warped factor
must have SU(3) holonomy. The second unbroken susy condition
implies that the warped factor  in metric is 1 and the metric
in metric is 1 and the metric 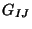 is unwarped.
Finally, the first condition implies that the dilation is constant.
This is a Calabi-Yau three-fold. A Calabi-Yau three-fold is also a Kähler manifold
in which the first Chern
class zero i.e.
is unwarped.
Finally, the first condition implies that the dilation is constant.
This is a Calabi-Yau three-fold. A Calabi-Yau three-fold is also a Kähler manifold
in which the first Chern
class zero i.e.
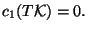 Any Calabi-Yau manifold possesses a unique Ricci-flat metric.
When we
consider
Any Calabi-Yau manifold possesses a unique Ricci-flat metric.
When we
consider  heterotic string theory on Calabi-Yau three-fold we obtain a
four-dimensional chiral theory with spacetime supersymmetry
heterotic string theory on Calabi-Yau three-fold we obtain a
four-dimensional chiral theory with spacetime supersymmetry 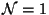 .
In fact, compactification on manifolds of SU(3) holonomy preserves
.
In fact, compactification on manifolds of SU(3) holonomy preserves 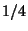 of
supersymmetry. If we consider
of
supersymmetry. If we consider 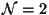 theories (for example, type II
superstrings) in
theories (for example, type II
superstrings) in
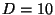 dimensions, after compactification on a Calabi-Yau three-fold we obtain
dimensions, after compactification on a Calabi-Yau three-fold we obtain 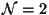 theories in
theories in  .
In addition to the CY-threefold structure for
.
In addition to the CY-threefold structure for  the unbroken susy condition
the unbroken susy condition
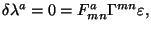 leads to the equations in complex
coordinates
leads to the equations in complex
coordinates
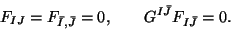 |
(28) |
These equations require to specify a gauge subbundle 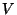 of a
of a
 gauge bundle
over
gauge bundle
over  and a gauge connection
and a gauge connection 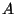 on
on 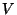 with curvature
with curvature 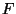 . The condition
. The condition
 tell us that the subbundle
tell us that the subbundle 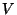 as well as the
corresponding connection should be holomorphic. The second condition
as well as the
corresponding connection should be holomorphic. The second condition
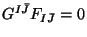 is the celebrated Donaldson-Uhlenbeck-Yau equation for
is the celebrated Donaldson-Uhlenbeck-Yau equation for 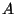 . This equation has a
unique solution if the bundle
. This equation has a
unique solution if the bundle 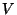 is stable and if it is satisfied the integrability condition
is stable and if it is satisfied the integrability condition
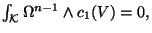 where
where 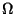 is the Kähler form of
is the Kähler form of
 . There is a further condition to be satisfied by the connection
. There is a further condition to be satisfied by the connection 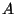 , the Bianchi
identity for
, the Bianchi
identity for  and
and 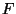 , it is given by
, it is given by
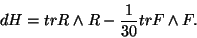 |
(29) |
The only solution is
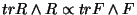 which implies that
which implies that
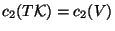 . This situation is usually known as the standard embedding of the spin connection
in the gauge connection ant it is a method to determine the connection
. This situation is usually known as the standard embedding of the spin connection
in the gauge connection ant it is a method to determine the connection 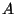 on
on 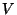 .
Thus in the compactification of phenomenological interest of the heterotic theory with the
ansatz
.
Thus in the compactification of phenomenological interest of the heterotic theory with the
ansatz
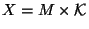 , the internal space has to be a Calabi-Yau three-fold and one
has to specify a stable, holomorphic vector bundle
, the internal space has to be a Calabi-Yau three-fold and one
has to specify a stable, holomorphic vector bundle 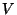 over
over 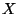 (or
(or  ) satisfying
) satisfying
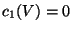 and
and
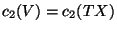 .
If
.
If 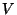 is a SU
is a SU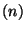 vector bundle over
vector bundle over 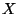 the subgroups of
the subgroups of
 that
commutes are
that
commutes are 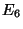 , SO(10) and SU(5) for
, SO(10) and SU(5) for 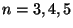 respectively. This leads to
GUTs in four dimensions justly with the gauge groups
respectively. This leads to
GUTs in four dimensions justly with the gauge groups 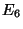 , SO(10) or SU(5).
truecm
Massless Spectrum
In order to describe the impact of the characteristics of
, SO(10) or SU(5).
truecm
Massless Spectrum
In order to describe the impact of the characteristics of  and
and 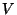 on the
properties of the spectrum of the four dimensional theory we start by decomposing
the ten-dimensional Dirac operator under
on the
properties of the spectrum of the four dimensional theory we start by decomposing
the ten-dimensional Dirac operator under
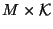 into
into
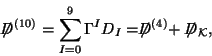 |
(30) |
where
 and
and
 . Dirac equation in ten dimensions is
. Dirac equation in ten dimensions is
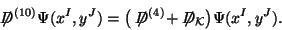 |
(31) |
Thus the spectrum of the Dirac operator
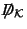 on
on  determines
the massive spectrum of fermions in four dimensions.
In ten dimensions the Lorentz group only has real spinor representations and
the Clifford modules decomposes as:
determines
the massive spectrum of fermions in four dimensions.
In ten dimensions the Lorentz group only has real spinor representations and
the Clifford modules decomposes as:
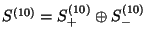 . Positive and negative chirality are distinguised by
. Positive and negative chirality are distinguised by
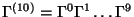 .
. 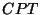 theorem implies that we must take
only one chirality
theorem implies that we must take
only one chirality
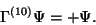 |
(32) |
Decompose the spinor representation of SO(1,9) under
 with
with
 where
where
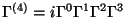 and
and
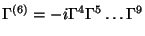 .
One solution with
.
One solution with
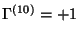 is given by
is given by
 and then the spin
bundle decomposes
under
and then the spin
bundle decomposes
under
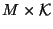 as
as
 |
(33) |
Now solve the Dirac equation with the ansatz
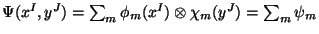 and
and
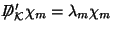 . It leads to
. It leads to
 |
(34) |
where
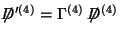 and
and
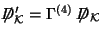 .
.
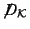 is an
elliptic operator on the
compact manifold
is an
elliptic operator on the
compact manifold  , this implies that that operator has a finite number of
fermion zero modes. Massless fermions in four dimensions originate as zero
modes of the Dirac operators
, this implies that that operator has a finite number of
fermion zero modes. Massless fermions in four dimensions originate as zero
modes of the Dirac operators
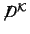 of the internal manifold
of the internal manifold  . By
the
Atiyah-Singer theorem, a topological invariant of
. By
the
Atiyah-Singer theorem, a topological invariant of  containing the information of
the chiral fermions on
containing the information of
the chiral fermions on  is given by the index of the Dirac operator
is given by the index of the Dirac operator
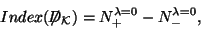 |
(35) |
for chiral fermions on  with
with
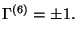 Here
Here
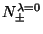 are the number of positive and negative chiral zero modes. In
are the number of positive and negative chiral zero modes. In  dimensions
this index is vanishing. We need to couple gauge fields coming from the heterotic string
theory. Recall that they are
dimensions
this index is vanishing. We need to couple gauge fields coming from the heterotic string
theory. Recall that they are
 valued gauge fields.
The standard embedding of the
spin connection in the gauge connection leads to the chain of maximal subgroups:
valued gauge fields.
The standard embedding of the
spin connection in the gauge connection leads to the chain of maximal subgroups:
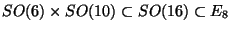 . This breaks SO(16) to SO(10). The computation of the
. This breaks SO(16) to SO(10). The computation of the 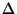 for this case yields
for this case yields
 where
where  are irreps of
SO(6) and
are irreps of
SO(6) and  are complex irreps of SO(10). These latter determine the irreps where are
distributed the massless fermions of the four-dimensional theory. The former irreps
are complex irreps of SO(10). These latter determine the irreps where are
distributed the massless fermions of the four-dimensional theory. The former irreps 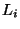 determine
the number of fermionic chiral zero modes described by the topological index
determine
the number of fermionic chiral zero modes described by the topological index
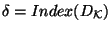 . This is given by
. This is given by
and from the solution
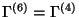 it determines the chiral fermion families in four
dimensions
it determines the chiral fermion families in four
dimensions
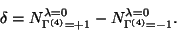 |
(36) |
Thus the theory in four dimensions has
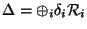 where
where
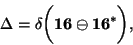 |
(37) |
where
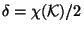 with
with
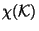 is the Euler number of
is the Euler number of 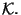 truecm
truecm



Next: T-duality, D-branes and Brane
Up: Perturbative String and Superstring
Previous: Heterotic Superstrings
root
2001-01-15