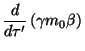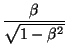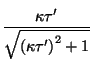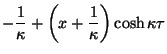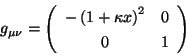Next: Gravedad y relatividad especial
Up: DE LA RELATIVIDAD ESPECIAL
Previous: DE LA RELATIVIDAD ESPECIAL
Índice General
La relatividad especial se puede utilizar para describir los eventos tal
como son vistos por un observador en un marco de referencia acelerado. Para
este propósito se considera que el sistema 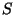 se mueve con una
partícula de masa
se mueve con una
partícula de masa 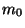 a lo largo del eje
a lo largo del eje 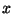 positivo del sistema
positivo del sistema
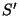 . La partícula se somete a una fuerza
. La partícula se somete a una fuerza 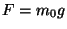 en
dirección del eje
en
dirección del eje 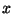 . La ecuación de movimiento para dicha
partícula será
. La ecuación de movimiento para dicha
partícula será
en donde
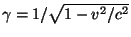 ,
,
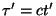 y
y
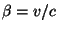 corresponde a la velocidad instantánea entre
corresponde a la velocidad instantánea entre 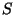 y
y
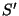 . La última de las ecs. 2.1 se puede integrar
directamente. En el primer miembro la variable es la velocidad
. La última de las ecs. 2.1 se puede integrar
directamente. En el primer miembro la variable es la velocidad 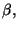 la
cual se valúa desde cero hasta un valor
la
cual se valúa desde cero hasta un valor 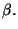 En el segundo miembro
la variable
En el segundo miembro
la variable
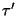 se valúa, de igual manera, desde cero a un
tiempo
se valúa, de igual manera, desde cero a un
tiempo
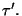 Con esto se llega a que2.1
Con esto se llega a que2.1
Sustituyendo
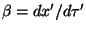 en la ecuación
anterior e integrando sobre
en la ecuación
anterior e integrando sobre 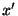 desde una posición
desde una posición
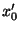 hasta
hasta 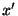 y sobre el tiempo desde cero hasta
y sobre el tiempo desde cero hasta
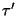 se obtiene
se obtiene
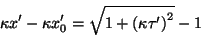 |
(2.3) |
lo cual se puede escribir como
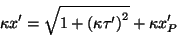 |
(2.4) |
donde
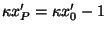 y
y 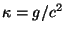 .
La ecuación anterior expresa la posición de la partícula como
función del tiempo en el sistema
.
La ecuación anterior expresa la posición de la partícula como
función del tiempo en el sistema 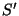 . De las ecs. 2.1 y 2.4 se puede deducir que las ecuaciones de
transformación entre un sistema acelerado y un sistema inercial son
. De las ecs. 2.1 y 2.4 se puede deducir que las ecuaciones de
transformación entre un sistema acelerado y un sistema inercial son
De estas ecuaciones se puede obtener el tensor métrico para el sistema
acelerado, el cual es
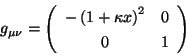 |
(2.6) |
con esto, la métrica se escribe de la forma
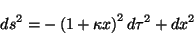 |
(2.7) |
Es importante observar algunos hechos implícitos en esta métrica.
Por ejemplo, si 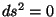 se tiene que
se tiene que
es decir, que la velocidad de la luz depende ahora de la posición. Es
más, cuando 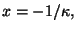 se tiene que
se tiene que 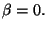 El evento en
El evento en
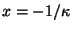 nunca será observado porque la luz nunca escapa de
allí, justo como en la superficie de un agujero negro. Estos hechos
parecen contradecir los principios de la relatividad especial pero en
realidad no es así, puesto que estos principios se aplican a
observadores en marcos de refencia inercial. Las consecuencias de la ec. 2.8 serán verificadas para un observador en un marco
acelerado, para el cuál, los principios de la relatividad especial ya no
son válidos.[3]
nunca será observado porque la luz nunca escapa de
allí, justo como en la superficie de un agujero negro. Estos hechos
parecen contradecir los principios de la relatividad especial pero en
realidad no es así, puesto que estos principios se aplican a
observadores en marcos de refencia inercial. Las consecuencias de la ec. 2.8 serán verificadas para un observador en un marco
acelerado, para el cuál, los principios de la relatividad especial ya no
son válidos.[3]




Next: Gravedad y relatividad especial
Up: DE LA RELATIVIDAD ESPECIAL
Previous: DE LA RELATIVIDAD ESPECIAL
Índice General
enrique pazos
2000-09-27