


Next: The CDM spectrum.
Up: Non-baryonic models
Previous: Non-baryonic models
In the hot dark matter (HDM) model the mass contained inside the horizon
when constituent particles become non relativistic is much larger than the
typical mass of a galaxy (
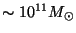 ), so that particles with a low
mass are required. A natural candidate for HDM constituent is the massive
neutrino. If a neutrino species has non vanishing mass, then its
contribution to the mean matter density is
), so that particles with a low
mass are required. A natural candidate for HDM constituent is the massive
neutrino. If a neutrino species has non vanishing mass, then its
contribution to the mean matter density is
 |
(33) |
where 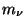 is expressed in
is expressed in 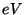 . Although in the classical version
of the Standard Model for the electroweak interaction the neutrino is
considered massless, nevertheless there exists no fundamental reason
which fixes
. Although in the classical version
of the Standard Model for the electroweak interaction the neutrino is
considered massless, nevertheless there exists no fundamental reason
which fixes 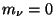 . Viceversa, several theoretical models have
been proposed to generate a non-vanishing neutrino mass
[37,14]. Although recent experimental evidences
are actually indicating that at least one neutrino species should be
massive [32], its mass could be too small to be
cosmologically relevant.
. Viceversa, several theoretical models have
been proposed to generate a non-vanishing neutrino mass
[37,14]. Although recent experimental evidences
are actually indicating that at least one neutrino species should be
massive [32], its mass could be too small to be
cosmologically relevant.
For a neutrino of mass 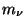 , the redshift at which it becomes
non-relativistic can be estimated to be
, the redshift at which it becomes
non-relativistic can be estimated to be
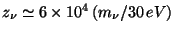 , which corresponds to
, which corresponds to
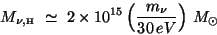 |
(34) |
for the mass contained inside the horizon at that epoch. Numerical
calculations carried out by Bond & Szalay [6] give the
transmission factor
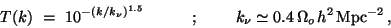 |
(35) |
which suppresses all the fluctuation modes at wavelengths
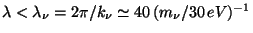 Mpc.
In the HDM scenario, the smallest
fluctuations surviving recombination are roughly on the same scale as large
galaxy clusters. Accordingly, structure formations proceeds in a
``top-down" way; first large pancakes of mass
Mpc.
In the HDM scenario, the smallest
fluctuations surviving recombination are roughly on the same scale as large
galaxy clusters. Accordingly, structure formations proceeds in a
``top-down" way; first large pancakes of mass
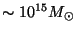 form,
while galaxies originate later via fragmentation of structures at larger
scales. Numerical simulations of structure formation in HDM dominated
Universe have been done [36] and show the development of
cellular structures, which are promisingly similar to those displayed by
the redshift galaxy surveys. Big voids forms on scales comparable to the
characteristic scale
form,
while galaxies originate later via fragmentation of structures at larger
scales. Numerical simulations of structure formation in HDM dominated
Universe have been done [36] and show the development of
cellular structures, which are promisingly similar to those displayed by
the redshift galaxy surveys. Big voids forms on scales comparable to the
characteristic scale  , which are surrounded by galaxies and
clusters forming at the intersection between three of such cells.
Unfortunately, the agreement with the observed galaxy distribution is only
apparent. In fact, since the characteristic size of the earliest forming
structures is
, which are surrounded by galaxies and
clusters forming at the intersection between three of such cells.
Unfortunately, the agreement with the observed galaxy distribution is only
apparent. In fact, since the characteristic size of the earliest forming
structures is  , the variance of the matter distribution at
this scale should be around one. This is quite difficult to reconcile with
the much smaller correlation length displayed by the galaxy distribution,
, the variance of the matter distribution at
this scale should be around one. This is quite difficult to reconcile with
the much smaller correlation length displayed by the galaxy distribution,
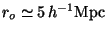 . In order to alleviate this problem, we can either assume
that galaxy formation occurred very recently (at
. In order to alleviate this problem, we can either assume
that galaxy formation occurred very recently (at
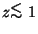 ) so as to
give no time for structures to become overclustered, or invoke some
mechanism to reduce the galaxy clustering with respect to that of the
underlying matter. It is however clear that, whatever way out we choose,
additional problems arise. A too recent galaxy formation seems to be quite
difficult to reconcile with the detection of high-redshift (
) so as to
give no time for structures to become overclustered, or invoke some
mechanism to reduce the galaxy clustering with respect to that of the
underlying matter. It is however clear that, whatever way out we choose,
additional problems arise. A too recent galaxy formation seems to be quite
difficult to reconcile with the detection of high-redshift (
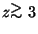 )
quasars. Also requiring
that galaxies are less clustered than matter is at variance with the
expectation that dissipative galaxy formation should preferentially occur
in the deep wells of the gravitational potential field, which would give an
increase of their correlation with respect to the DM distribution.
It is however clear that, if a
neutrino species were discovered to have a non-vanishing mass
)
quasars. Also requiring
that galaxies are less clustered than matter is at variance with the
expectation that dissipative galaxy formation should preferentially occur
in the deep wells of the gravitational potential field, which would give an
increase of their correlation with respect to the DM distribution.
It is however clear that, if a
neutrino species were discovered to have a non-vanishing mass
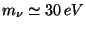 , we are obliged to consider HDM as responsible for structure
formation and try to overcome in some way all the above difficulties.
, we are obliged to consider HDM as responsible for structure
formation and try to overcome in some way all the above difficulties.



Next: The CDM spectrum.
Up: Non-baryonic models
Previous: Non-baryonic models
Waleska Aldana Segura
2001-01-16
![]() , the redshift at which it becomes
non-relativistic can be estimated to be
, the redshift at which it becomes
non-relativistic can be estimated to be
![]() , which corresponds to
, which corresponds to