


Next: N-body simulations
Up: Non-baryonic models
Previous: The HDM spectrum.
The dark matter content of the Universe is said to be cold if particles
becomes non-relativistic at sufficiently early times, so that the mass
contained within the horizon at that time is much smaller than the typical
galaxy mass. Thus, in the cold dark matter (CDM) scenario the
free-streaming cut-off scale is to small to be of any cosmological
relevance. The low velocity required for CDM particles can arise for two
different reasons. Firstly, the particle mass is so large that they become
non relativistic at a high temperature. This cannot be the case for massive
neutrinos, for which a mass
 give an exceedingly high
contribution to the density parameter (see eq.[33]). However,
supersymmetric theories provide a large variety of exotic CDM candidates,
such as photinos or gravitinos, with masses above
give an exceedingly high
contribution to the density parameter (see eq.[33]). However,
supersymmetric theories provide a large variety of exotic CDM candidates,
such as photinos or gravitinos, with masses above  . Secondly, there
can be particles, like axions, that never were in thermal equilibrium, so
they have a very low thermal velocity, despite their small mass (
. Secondly, there
can be particles, like axions, that never were in thermal equilibrium, so
they have a very low thermal velocity, despite their small mass (
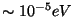 ). See, e.g., ref.[12] for a review of CDM
candidates.
). See, e.g., ref.[12] for a review of CDM
candidates.
Although for CDM fluctuations neither free-streaming nor Silk damping
introduce characteristic scales, a distortion of the spectrum is
however generated by the Meszaros effect [23], which
suppresses the growth of fluctuations of non-relativistic matter which
cross the horizon before non-relativistic matter start dominating. In
order to see how this happens, let us consider the equation for the
evolution of non-relativistic matter fluctuations in a relativistic
background:
 |
(36) |
Here the relativistic background enters only in determining the cosmic
expansion rate 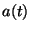 . By introducing the new time variable
. By introducing the new time variable
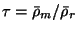 (
(
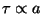 since
since
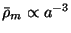 and
and
 ), eq.(36) can be rewritten as
), eq.(36) can be rewritten as
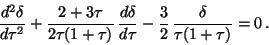 |
(37) |
The growing-mode solution of the above equation turns out to be
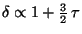 . Thus, during radiation domination (
. Thus, during radiation domination ( ), the fluctuation amplitude is frozen. Only when non-relativistic matter
dominates (
), the fluctuation amplitude is frozen. Only when non-relativistic matter
dominates ( ) the matter fluctuations start growing as
) the matter fluctuations start growing as
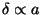 , as expected on the grounds of linear evolution. In order to
evaluate the resulting distortion of the spectrum, let
, as expected on the grounds of linear evolution. In order to
evaluate the resulting distortion of the spectrum, let 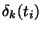 be
the amplitude of the fluctuation mode with wavenumber
be
the amplitude of the fluctuation mode with wavenumber  at some initial
time
at some initial
time 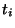 before matter-radiation equality, and suppose that it crosses
the horizon at
before matter-radiation equality, and suppose that it crosses
the horizon at 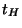 , also before equality. During this period the
amplitude grows by a factor
, also before equality. During this period the
amplitude grows by a factor 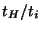 . Since
. Since
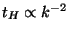 during
radiation domination, the amplitude of the perturbation after horizon
crossing is frozen at the value
during
radiation domination, the amplitude of the perturbation after horizon
crossing is frozen at the value
 until matter
starts dominating. Viceversa, fluctuations outside the horizon continue to
grow according to linear theory so that no distortion of the spectrum
occurs at such scales. The characteristic scale at which we expect a
feature in the spectrum is that corresponding to the horizon size at
until matter
starts dominating. Viceversa, fluctuations outside the horizon continue to
grow according to linear theory so that no distortion of the spectrum
occurs at such scales. The characteristic scale at which we expect a
feature in the spectrum is that corresponding to the horizon size at
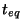 ,
,
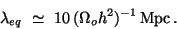 |
(38) |
If
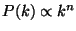 was the primordial spectrum, its shape after
was the primordial spectrum, its shape after
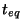 will be preserved at scales larger than
will be preserved at scales larger than 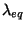 , while
for
, while
for
 the freezing of the fluctuation
amplitude tilts the spectral index to the value
the freezing of the fluctuation
amplitude tilts the spectral index to the value  . Precise
computations of the processed spectrum in a CDM dominated Universe
have been done by several groups (see, e.g., refs.[11]
and references therein).
A useful fit to the CDM transfer function can be given in the form
. Precise
computations of the processed spectrum in a CDM dominated Universe
have been done by several groups (see, e.g., refs.[11]
and references therein).
A useful fit to the CDM transfer function can be given in the form
![\begin{displaymath}
T(k) = [1+(ak+(bk)^{1.5}+(ck)^2)^\nu]^{-1/\nu}
\end{displaymath}](img190.gif) |
(39) |
[
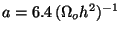 Mpc,
Mpc,
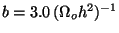 Mpc,
Mpc,
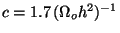 Mpc,
Mpc, 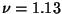 ], obtained by Bond &
Efstathiou [5], assuming the presence of three species of
massless neutrinos and negligible contribution from the baryonic
component (
], obtained by Bond &
Efstathiou [5], assuming the presence of three species of
massless neutrinos and negligible contribution from the baryonic
component (
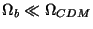 ).
According to eq.(39), as
).
According to eq.(39), as 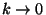 , we have
, we have  and the primordial spectrum
and the primordial spectrum  is left unchanged. At small scales,
is left unchanged. At small scales,
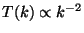 , so that
, so that
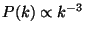 .
.
As opposed to the HDM scenario, a considerable amount of small-scale
power is now present, so that the first fluctuations reaching
non-linearity are at small scales. The resulting clustering proceeds
in a ``bottom-up" way, with structures of increasing size forming from
the tidal interaction and the merging of smaller structures. It is
clear that the possibility for small-scale structures not to be
disrupted as the hierarchical clustering goes on depends on the
ability of the baryonic component to cool down and fully virialize
before being incorporated within larger DM fluctuations. Taking into
account dissipative effects allows one to identify the CDM
fluctuations where galaxy formation takes place. Detailed
investigations of galaxy formation in the CDM scenario (see, e.g., ref.[30]) have shown that the observed variety of
galaxy morphology and the relative morphological segregation of the
clustering can be nicely reproduced.
A series of detailed numerical simulations of structure formation in a
CDM Universe have been realized (see, e.g.,
ref.[19]). The N-body experiments show that the primordial
CDM spectrum is able to account for many aspects of the observed
galaxy clustering at small and intermediate scales. Once a suitable
prescription is assigned to identify galaxies in a purely
dissipationless simulation, a CDM model with 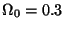 and
flatness restored by a cosmological constant term provides the correct
correlation amplitudes, small-scale velocity dispersions and the mean
number density of both galaxies and clusters.
and
flatness restored by a cosmological constant term provides the correct
correlation amplitudes, small-scale velocity dispersions and the mean
number density of both galaxies and clusters.



Next: N-body simulations
Up: Non-baryonic models
Previous: The HDM spectrum.
Waleska Aldana Segura
2001-01-16
![]() and
flatness restored by a cosmological constant term provides the correct
correlation amplitudes, small-scale velocity dispersions and the mean
number density of both galaxies and clusters.
and
flatness restored by a cosmological constant term provides the correct
correlation amplitudes, small-scale velocity dispersions and the mean
number density of both galaxies and clusters.