


Next: Parenthesis on Global and
Up: Examples
Previous: The Intermediate Vector Boson
Parenthesis on the Minimal Interaction
The study of the movement of charged particles in an
electromagnetic field exemplifies the treatment of a non-conservative
system as the potential depends on the velocity.
Nevertheless, for this system the equations of Euler-Lagrange can be
written
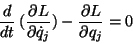 |
(127) |
with
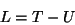 |
(128) |
and 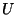 , the generalized potential which gives place to the generalized
forces
, the generalized potential which gives place to the generalized
forces
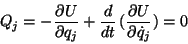 |
(129) |
as
![\begin{displaymath}
\vec{F} = q [\vec{E} + \frac{1}{c} (\vec{v}\wedge \vec{B})]
\end{displaymath}](img321.gif) |
(130) |
it can be written
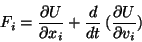 |
(131) |
with
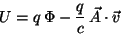 |
(132) |
in such a way that
 |
(133) |
>From the knowledge of 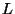 , the Hamiltonian formalism can be
followed but with no possible way of insuring a priori that
, the Hamiltonian formalism can be
followed but with no possible way of insuring a priori that 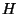 coincides with the total energy. Nevertheless, that is the case
for the electromagnetism (why?).
coincides with the total energy. Nevertheless, that is the case
for the electromagnetism (why?).
From 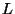 , the canonical momentum results
, the canonical momentum results
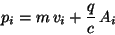 |
(134) |
and then
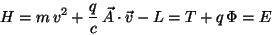 |
(135) |
The Hamiltonian can be written then in terms of the canonical
momentum as
![\begin{displaymath}
H = \frac{1}{2 m} \left[\vec{p} -
\frac{q}{c} \vec{A}\right]^{2} + q \Phi
\end{displaymath}](img329.gif) |
(136) |
that is also a
valid form for the relativistic case.
A recipe can then be formalized: The Hamiltonian of a charged
particle in an electromagnetic field is obtained from the case for a
generic 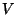 potential, through the replacement
potential, through the replacement
which is called minimal interaction.
The quantum mechanics of a charged particle in an electromagnetic
field is obtained,
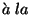 Schrödinger, translating
operationally the Hamiltonian written in terms of the coordinate
and the canonical momentum. In that way the Schrödinger
equation arises
Schrödinger, translating
operationally the Hamiltonian written in terms of the coordinate
and the canonical momentum. In that way the Schrödinger
equation arises
![\begin{displaymath}
i \hbar \frac{\partial \psi}{\partial
t}(\vec{r},t) =
\lef...
...ac{q}{c} \vec{A}\right)^{2} + q \Phi\right] \psi(\vec{r},t)
\end{displaymath}](img335.gif) |
(139) |
For QED, theory of electrons and photons,
the Lagrangian is
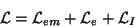 |
(140) |
with
and
![\begin{displaymath}
{\cal L}_{I} = - e \bar{\psi} \gamma_{\mu} A^{\mu} \psi \;\;\; [minimal]
\end{displaymath}](img340.gif) |
(143) |
Again, the minimal electromagnetic interaction comes from
replacing in the equation of motion of the electron
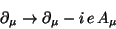 |
(144) |
This replacement is entirely analogous to the one of the quantum mechanics
and gives place to a renormalizable theory. We could certainly think
of a more general interaction (not minimal). For example of the type
which has the required properties but gives rise to a non-renormalizable
theory.
It will be then a challenge to provide a theoretical background
for the presence of the minimal interaction in the electromagnetic
case and try to generalize the idea to the other
interactions. The recent developments are based on symmetry
requierements to be fullfilled by the theoretical structure. This
is the origin of Gauge Theories.



Next: Parenthesis on Global and
Up: Examples
Previous: The Intermediate Vector Boson
root
2001-01-22
![]() , the Hamiltonian formalism can be
followed but with no possible way of insuring a priori that
, the Hamiltonian formalism can be
followed but with no possible way of insuring a priori that ![]() coincides with the total energy. Nevertheless, that is the case
for the electromagnetism (why?).
coincides with the total energy. Nevertheless, that is the case
for the electromagnetism (why?).
![]() , the canonical momentum results
, the canonical momentum results
![]() potential, through the replacement
potential, through the replacement
![]() Schrödinger, translating
operationally the Hamiltonian written in terms of the coordinate
and the canonical momentum. In that way the Schrödinger
equation arises
Schrödinger, translating
operationally the Hamiltonian written in terms of the coordinate
and the canonical momentum. In that way the Schrödinger
equation arises
![\begin{displaymath}
i \hbar \frac{\partial \psi}{\partial
t}(\vec{r},t) =
\lef...
...ac{q}{c} \vec{A}\right)^{2} + q \Phi\right] \psi(\vec{r},t)
\end{displaymath}](img335.gif)