


Next: Phase Invariance
Up: Examples
Previous: Parenthesis on the Minimal
Starting from our consideration of symmetry as an aesthetic
cultural necessity, we are going to try now to think of symmetry
as a source of the fundamental interactions. Let us remember that
the existence of a symmetry implies the existence of a
conservation law. In fact, given a Lagrangian
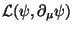 which verifies
which verifies
 |
(145) |
when
a change  due to variations of continuous parameters
is performed,it suffer a variation:
due to variations of continuous parameters
is performed,it suffer a variation:
![\begin{displaymath}
\delta {\cal L} =
\partial_{\mu} \left[\frac{\partial {\cal L}}{\partial
(\partial_{\mu}\psi)} \delta \psi\right]
\end{displaymath}](img346.gif) |
(146) |
now, if 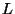 is
symmetric (invariant) with respect to the change
is
symmetric (invariant) with respect to the change  ,
that is
,
that is
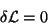 |
(147) |
there results the Noether
theorem: a current is conserved
![\begin{displaymath}
\partial_{\mu}J^{\mu} = \partial_{\mu}\left[\frac{\partial {\cal L}}{\partial
(\partial_{\mu}\psi)} \delta\psi\right] = 0
\end{displaymath}](img348.gif) |
(148) |
For example, the invariance of 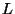 with respect to traslations implies the
conservation of the momentum and of the energy. The invariance in front
of rotations gives place to the conservation of the angular momentum,
etc. We are then in the presence of continuous groups of symmetry. In
the first case we have a four parameter group:
with respect to traslations implies the
conservation of the momentum and of the energy. The invariance in front
of rotations gives place to the conservation of the angular momentum,
etc. We are then in the presence of continuous groups of symmetry. In
the first case we have a four parameter group:
 , the displacements.
In the case of the rotations is a three parameter group, the angles,
etc. In the general case we will be leading with a continuous group of
symmetries of the Lagrangian which will depend on
, the displacements.
In the case of the rotations is a three parameter group, the angles,
etc. In the general case we will be leading with a continuous group of
symmetries of the Lagrangian which will depend on 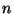 parameters
parameters
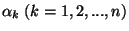 . The general case can go beyond the space-time
symmetries of the previous examples and can refer to symmetries
linked to the formalism own structure: the internal symmetries.
. The general case can go beyond the space-time
symmetries of the previous examples and can refer to symmetries
linked to the formalism own structure: the internal symmetries.



Next: Phase Invariance
Up: Examples
Previous: Parenthesis on the Minimal
root
2001-01-22
![]() which verifies
which verifies
![]() with respect to traslations implies the
conservation of the momentum and of the energy. The invariance in front
of rotations gives place to the conservation of the angular momentum,
etc. We are then in the presence of continuous groups of symmetry. In
the first case we have a four parameter group:
with respect to traslations implies the
conservation of the momentum and of the energy. The invariance in front
of rotations gives place to the conservation of the angular momentum,
etc. We are then in the presence of continuous groups of symmetry. In
the first case we have a four parameter group:
![]() , the displacements.
In the case of the rotations is a three parameter group, the angles,
etc. In the general case we will be leading with a continuous group of
symmetries of the Lagrangian which will depend on
, the displacements.
In the case of the rotations is a three parameter group, the angles,
etc. In the general case we will be leading with a continuous group of
symmetries of the Lagrangian which will depend on ![]() parameters
parameters
![]() . The general case can go beyond the space-time
symmetries of the previous examples and can refer to symmetries
linked to the formalism own structure: the internal symmetries.
. The general case can go beyond the space-time
symmetries of the previous examples and can refer to symmetries
linked to the formalism own structure: the internal symmetries.