


Next: Local Latent Symmetry: Higgs
Up: Latent Symmetry
Previous: Discrete Global Latent Symmetry
The generalization of the previous model to the case of a
continuous symmetry is represented by the so called Goldstone model
defined by the Lagrangian
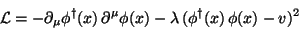 |
(244) |
where  is a complex scalar field. This Lagrangian is invariant
under phase transformations
is a complex scalar field. This Lagrangian is invariant
under phase transformations
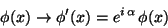 |
(245) |
with 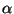 constant. That is to say we are in front of a global symmetry
constant. That is to say we are in front of a global symmetry
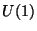 which gives place to the conserved current
which gives place to the conserved current
![\begin{displaymath}
J^{\mu}(x) = i [(\partial^{\mu}\phi^{\dagger}) \phi
- (\partial^{\mu} \phi) \phi^{\dagger}]
\end{displaymath}](img530.gif) |
(246) |
The potential that appears in (246)
 |
(247) |
depends on the sign of the constant 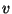 .
.
So if 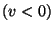 , the potential
presents only one minimum at
, the potential
presents only one minimum at  : the symmetry is realized
: the symmetry is realized
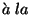 Wigner-Weyl.
Wigner-Weyl.
If on the contrary, 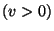 , we are in the presence of
an infinite number of minima defined by
, we are in the presence of
an infinite number of minima defined by
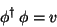 |
(248) |
which in terms of the fields 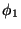 and
and 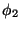 , real and imaginary
part of
, real and imaginary
part of 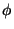 , respectively, it is written
, respectively, it is written
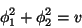 |
(249) |
and whose representation is the well-known ``culo de botella" or
``mexican hat".
Now, the symmetry (U(1) global) is done 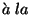 Nambu-
Goldstone. As a consequence of the already mentioned Goldstone theorem
the theory defined by the Lagrangian (246), when the symmetry is
latent, will contain a massless state: the Goldstone boson.
Nambu-
Goldstone. As a consequence of the already mentioned Goldstone theorem
the theory defined by the Lagrangian (246), when the symmetry is
latent, will contain a massless state: the Goldstone boson.
The uniform movement (constant hunger) of the donkey in the circle of
carrots correponds to the non massive excitation called Goldstone
boson.
Coming back to the model, when 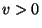 in the potential (249),
it has no sense the development around
in the potential (249),
it has no sense the development around  as there we are
in a local maximum. The perturbative development must be defined from a field
as there we are
in a local maximum. The perturbative development must be defined from a field
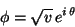 |
(250) |
with some 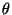 , arbitrary, due to the non unicity of the vacuum.
, arbitrary, due to the non unicity of the vacuum.
Certainly, the latent symmetry 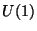 allows to eliminate
allows to eliminate 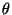 because
because
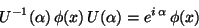 |
(251) |
choosing
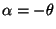 and considering (252)
and considering (252)
 |
(252) |
as
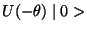 is equivalent to
is equivalent to 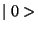 due to the latent
character of the symmetry.
due to the latent
character of the symmetry.
In a similar way to the case of the discrete symmetry, after
choosing a perturbative vacuum the field 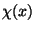 is defined with
is defined with
 |
(253) |
through
 |
(254) |
The potential in terms of 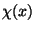 results
results
 |
(255) |
Introducing now the fields 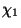 and
and 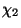 , real and imaginary
parts of
, real and imaginary
parts of 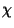 respectively, it is easy to see that
respectively, it is easy to see that 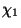 is a massive
field with
is a massive
field with
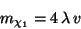 |
(256) |
while
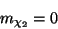 |
(257) |
allowing us to conclude that the field 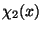 corresponds
precisely to the Goldstone boson.
The results (258) and (259) show that when the symmetry (U(1)
in the example) is latent or spontaneously broken it will not be
present in the spectrum of the theory.
corresponds
precisely to the Goldstone boson.
The results (258) and (259) show that when the symmetry (U(1)
in the example) is latent or spontaneously broken it will not be
present in the spectrum of the theory.
The previous results become more intuitive if the field 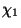 is
assimilated with radial excitations around a point in the minimum
circle, meanwhile
is
assimilated with radial excitations around a point in the minimum
circle, meanwhile 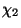 corresponds to the movement, with zero frequency,
around this circle. In fact, if the field variables of angular type
(polar coordinates) are introduced
corresponds to the movement, with zero frequency,
around this circle. In fact, if the field variables of angular type
(polar coordinates) are introduced
The phase transformation 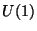 (247) corresponds then to
(247) corresponds then to
and the Lagrangian of the model is written
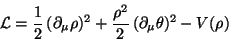 |
(262) |
so that the phase invariance is shown in the independence of 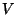 with
the variable
with
the variable 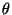 . If the vacuum is chosen in
. If the vacuum is chosen in
and the displaced fields are introduced
the Lagrangian results
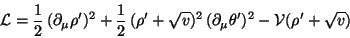 |
(267) |
As the field 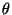 appears only through its derivative it is concluded
that its quantums will be massless and as it was already mentioned, it
corresponds to rotations around the minimal circle. The previous
discussion shows also that the appearance of the Goldstone boson is
directly linked to the spontaneous breaking of the symmetry and does
not depend of the particular form of the potential
appears only through its derivative it is concluded
that its quantums will be massless and as it was already mentioned, it
corresponds to rotations around the minimal circle. The previous
discussion shows also that the appearance of the Goldstone boson is
directly linked to the spontaneous breaking of the symmetry and does
not depend of the particular form of the potential 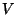 (or
(or  ).
).



Next: Local Latent Symmetry: Higgs
Up: Latent Symmetry
Previous: Discrete Global Latent Symmetry
root
2001-01-22
![]() , the potential
presents only one minimum at
, the potential
presents only one minimum at ![]() : the symmetry is realized
: the symmetry is realized
![]() Wigner-Weyl.
Wigner-Weyl.
![]() , we are in the presence of
an infinite number of minima defined by
, we are in the presence of
an infinite number of minima defined by
![]() Nambu-
Goldstone. As a consequence of the already mentioned Goldstone theorem
the theory defined by the Lagrangian (246), when the symmetry is
latent, will contain a massless state: the Goldstone boson.
Nambu-
Goldstone. As a consequence of the already mentioned Goldstone theorem
the theory defined by the Lagrangian (246), when the symmetry is
latent, will contain a massless state: the Goldstone boson.
![]() in the potential (249),
it has no sense the development around
in the potential (249),
it has no sense the development around ![]() as there we are
in a local maximum. The perturbative development must be defined from a field
as there we are
in a local maximum. The perturbative development must be defined from a field
![]() allows to eliminate
allows to eliminate ![]() because
because
![]() is defined with
is defined with
![]() results
results
![]() and
and ![]() , real and imaginary
parts of
, real and imaginary
parts of ![]() respectively, it is easy to see that
respectively, it is easy to see that ![]() is a massive
field with
is a massive
field with
![]() is
assimilated with radial excitations around a point in the minimum
circle, meanwhile
is
assimilated with radial excitations around a point in the minimum
circle, meanwhile ![]() corresponds to the movement, with zero frequency,
around this circle. In fact, if the field variables of angular type
(polar coordinates) are introduced
corresponds to the movement, with zero frequency,
around this circle. In fact, if the field variables of angular type
(polar coordinates) are introduced
![]() appears only through its derivative it is concluded
that its quantums will be massless and as it was already mentioned, it
corresponds to rotations around the minimal circle. The previous
discussion shows also that the appearance of the Goldstone boson is
directly linked to the spontaneous breaking of the symmetry and does
not depend of the particular form of the potential
appears only through its derivative it is concluded
that its quantums will be massless and as it was already mentioned, it
corresponds to rotations around the minimal circle. The previous
discussion shows also that the appearance of the Goldstone boson is
directly linked to the spontaneous breaking of the symmetry and does
not depend of the particular form of the potential ![]() (or
(or ![]() ).
).