In his paper ``A Theory of Leptons" published in Physical Review Letters in 1967, S. Weinberg says: ``Leptons interact only with photons and with the intermediate bosons which presumably mediate the weak interactions. What can be more natural than linking those one spin bosons in a multiplete of gauge fields?"
In this phrase we find the underlying idea for the model of Salam-Weinberg which we are going to develop now. We will certainly have to face several difficulties, already mentioned, as the mass difference between the photon and the intermediate bosons of the weak interactions. Besides, we must take into account that the electromagnetic and weak couplings are of very different intensity. The hope for success is based on the development of the theories with an spontaneously broken gauge symmetry which will allow to obtain a renormalizable model.
The first step in the construction of the model is the election
of the symmetry group ![]() .
.
The model must include the charged weak current
![]() , the
electromagnetic interaction linked to the group
, the
electromagnetic interaction linked to the group ![]() (that must be
unbroken as
(that must be
unbroken as ![]() ) and should also include a neutral weak current
) and should also include a neutral weak current
![]() that emerges a posteriori. Summarizing,
that emerges a posteriori. Summarizing, ![]() has to be a
four parameter group. The proposal arising from the model that is called
now Glashow-Salam-Weinberg electroweak model is
has to be a
four parameter group. The proposal arising from the model that is called
now Glashow-Salam-Weinberg electroweak model is
| (289) |
| (290) | |||
| (291) |
The ![]() model is chiral in the sense that
model is chiral in the sense that ![]() and
and ![]() behave differently under the gauge group
behave differently under the gauge group
![]() . In fact the left components form doublets
while the right components are singlets.
. In fact the left components form doublets
while the right components are singlets.
We begin analysing the charged weak current. As we saw when we
dealt with the weak interaction, this kind of currents must have ![]() structure, that is to say, only the fermionic fields of left chirality
will appear in its construction. In other words, the theory is a chiral
theory. We will have as an example
structure, that is to say, only the fermionic fields of left chirality
will appear in its construction. In other words, the theory is a chiral
theory. We will have as an example
| (292) |
It is clear that in each quark and lepton generation the same
quantum numbers of
![]() will be repeated. In particular,
in the first generation or electron family
will be repeated. In particular,
in the first generation or electron family
![]() , the pairs
, the pairs
![]() and
and ![]() will be
doublets of
will be
doublets of ![]() . That is to say, only the left parts carry contents
of
. That is to say, only the left parts carry contents
of ![]() as a consequence of the
as a consequence of the ![]() structure.
structure.
When it is pretended that the symmetry ![]() persists,
it must be required that
persists,
it must be required that
| (293) |
| (294) |
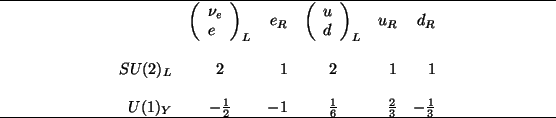
We can begin now to build a local (gauge) invariant Lagrangian under
![]() . In order to guarantee the local symmetry we must
introduce vector gauge fields. Due to
. In order to guarantee the local symmetry we must
introduce vector gauge fields. Due to ![]() , a triplet
, a triplet
![]() will be
needed and related to
will be
needed and related to ![]() the field
the field ![]() will be necessary.
will be necessary.
In terms of these gauge fields it is immediate to write the
covariant derivatives of the fermionic fields. For the first family it
results
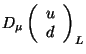 |
![$\displaystyle [\partial_{\mu} - i g_{1} \frac{1}{6} Y_{\mu} - i g_{2} \fra...
...{2}\cdot\vec{W}_{\mu}] \left( \begin{array}{c} u d \end{array} \right)_{L}$](img625.gif) |
(295) | |
| (296) | |||
| (297) | |||
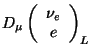 |
![$\displaystyle [\partial_{\mu} - i g_{1} \frac{1}{2} Y_{\mu} - i g_{2} \fra...
...ot\vec{W}_{\mu}] \left( \begin{array}{c} \nu_{e} e \end{array} \right)_{L}$](img631.gif) |
(298) | |
| (299) |
| (300) |
We then have that the Lagrangian ![]() for the first generation of
quarks and leptons is
for the first generation of
quarks and leptons is
| (302) |
| (303) |
Some of the interactions present in (303) can be summarized in the
expression
| (304) |
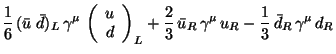 |
|||
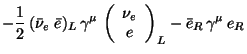 |
(305) |
| (306) |
The next question refers to the mass of the massive fermions.
We could propose first a typical Dirac mass Lagrangian as
The symmetry
![]() must be realized latent in a way to give
place to massive gauge fields. Nevertheless, this process must be
carefully done in order to guarantee that one of the final gauge
fields be correspondent with the massless photon. In other words, the
symmetry
must be realized latent in a way to give
place to massive gauge fields. Nevertheless, this process must be
carefully done in order to guarantee that one of the final gauge
fields be correspondent with the massless photon. In other words, the
symmetry
![]() cannot be fully broken. We must act in such a
way that
cannot be fully broken. We must act in such a
way that
As a consequence of the spontaneous symmetry breaking according to the
scheme (310), from the four initial gauge fields
![]() one ends with three
massive fields and one massless identifiable with the photon.
one ends with three
massive fields and one massless identifiable with the photon.
The photon, ![]() , is a combination of the neutral fields
, is a combination of the neutral fields
![]() and
and ![]() meanwhile the neutral combination orthogonal to the photon corresponds
to the intermediate boson of the neutral weak interactions,
meanwhile the neutral combination orthogonal to the photon corresponds
to the intermediate boson of the neutral weak interactions, ![]() , which
we mentioned above and should be massive.
Through the introduction of a mixing angle: the
Weinberg angle, we then write
, which
we mentioned above and should be massive.
Through the introduction of a mixing angle: the
Weinberg angle, we then write
| (309) | |||
| (310) |
It is useful to introduce the combinations of charged fields
| (311) |
In terms of these mediating fields of the electroweak forces, the
interactions are written
| (313) | |||
| (314) |
| (315) |
| (316) |
| (317) |
| (318) |
Let us return now to the explicit analysis of the spontaneous
symmetry breaking (310). We must trigger the Higgs mechanism. In order
to do it we introduce scalar fields, logically non trivial under the
group
![]() , so that its selfinteraction leads to a realization
of the symmetry
, so that its selfinteraction leads to a realization
of the symmetry ![]() Nambu-Goldstone.
The simplest election is a complex scalar field doublet of
Nambu-Goldstone.
The simplest election is a complex scalar field doublet of ![]() :
:
| (319) |
| (320) |
Due to the properties under
![]() of the field
of the field
![]() , its presence in
the Lagrangian of the theory will be of the form
, its presence in
the Lagrangian of the theory will be of the form
| (323) |
At this point it is easy to understand the appearance of the
masses of ![]() and of
and of ![]() . After the spontaneous symmetry breaking,
shifting from the field
. After the spontaneous symmetry breaking,
shifting from the field ![]() to the field
to the field ![]() satisfying
satisfying
We remember then, that
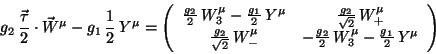 |
(326) |
 |
(327) |
| (328) |
In order to make things clearer, it is convenient to return again
to the exponential parametrization of the field ![]() , that is
, that is
| (332) |
| (333) |
Let us go now to the masses of quarks and leptons. It is clear
from above that here those masses also arise from the coupling of the
fermionic fields with the Higgs field ![]() , when we pass to the field
, when we pass to the field
![]() which verifies (326). The necessary couplings,
of the Yukawa type, are
written, for example for the quarks of the first generation
which verifies (326). The necessary couplings,
of the Yukawa type, are
written, for example for the quarks of the first generation
The Yukawa Lagrangian (336) can be written
| (335) |
| (336) |
At this point it is necessary to generalize the technique to give
mass to all the quarks and all the massive leptons. To do that,
another Higgs doublet is introduced, this time with ![]() ,
which works for the low members of the doublets, the fermions of
type
,
which works for the low members of the doublets, the fermions of
type ![]() . For this reason, the currents
. For this reason, the currents ![]() which
couple with
which
couple with ![]() are not diagonal in the generations,
although neutral currents are.
are not diagonal in the generations,
although neutral currents are.
We then introduce the usual notation
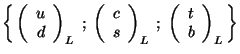 |
(337) | ||
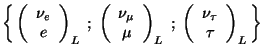 |
(338) | ||
| (339) | |||
| (340) | |||
| (341) |
| (343) |
It is clear from (344) that the coefficients ![]() are not diagonal in generation and besides, via the latent symmetry
a non diagonal mass matrix will arise
are not diagonal in generation and besides, via the latent symmetry
a non diagonal mass matrix will arise
| (344) |
The necessary diagonalization will provoke the mixing between the quark generations.
We introduce the notation
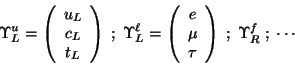 |
(345) |
| (346) |
Here we understand that the neutral currents are not affected because they are charge diagonal.
On the contrary, for the charged currents, for example for
| (348) |
| (349) |
We must emphasize that due to the supposed zero mass for the
neutrinos, the matrix
![]() in the second term can be eliminated
redefining
in the second term can be eliminated
redefining
![]() . In the first term the mixing matrix
of Cabibbo-Kobayashi-Maskawa is clearly defined
. In the first term the mixing matrix
of Cabibbo-Kobayashi-Maskawa is clearly defined
| (350) |
It is interesting at this point to present a test of coherence of
the spontaneous symmetry breaking mechanism in the sense of
verifying that the condition (310) has been respected. When the
symmetry is latent, the Higgs field verifies (323). Therefore, the
application of an operation of ![]() implies
implies
 |
(351) | ||
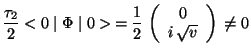 |
(352) | ||
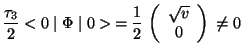 |
(353) |
| (354) |
That is to say none of the generators of
![]() annihilates the
vacuum. Nevertheless, the generator of
annihilates the
vacuum. Nevertheless, the generator of ![]() verifies
verifies
| (355) |
Let us try now a summary of ![]() in terms of the characteristic
parameters. In order to do that we write the limit of the model for
values of the momentum much lower than the mass of the gauge bosons. In
this case we will have to be able to contrast the resulting expression
with the Fermi effective Lagrangian at low energies. That is to
say
in terms of the characteristic
parameters. In order to do that we write the limit of the model for
values of the momentum much lower than the mass of the gauge bosons. In
this case we will have to be able to contrast the resulting expression
with the Fermi effective Lagrangian at low energies. That is to
say
Let us consider the propagator of ![]() or
or ![]() in the mentioned limit
in the mentioned limit
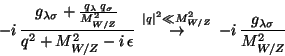 |
(357) |
| (358) | |||
| (359) |
These last two expressions, when compared to the effective
Lagrangian (358) allow to make the identifications
| (360) |
| (362) |
| (363) |
We bring here the experimental values of some of the parameters as a
reference
We also make a balance of the free parameters, to be fixed as the above mentioned from the experimental data:
It can be thought that these parameters should be
predicted from some super (or sub) structure underlying the ![]() model.
In any case it is a too large number of free parameters. Among them we
can call basic constants to the three couplings above (sometimes
model.
In any case it is a too large number of free parameters. Among them we
can call basic constants to the three couplings above (sometimes ![]() is choosen instead of
is choosen instead of
![]() ).
).
The electromagnetic constant ![]() is defined without ambiguity and
very accurately at
is defined without ambiguity and
very accurately at ![]() from Thomson scattering. This constant,
as all gauge coupling constants, is running with
from Thomson scattering. This constant,
as all gauge coupling constants, is running with ![]() . The Fermi constant
. The Fermi constant
![]() is also a very precise quantity measured in the
is also a very precise quantity measured in the ![]() decay.
Finally
decay.
Finally ![]() has recently been determined very accurately in LEP with
an error less than
has recently been determined very accurately in LEP with
an error less than ![]() .
.
It should be noticed that ![]() , the strong coupling constant
(the QCD coupling) also intervenes in the prediction
of several observables.
, the strong coupling constant
(the QCD coupling) also intervenes in the prediction
of several observables.
Nowadays, the most important unknown is the masses of the Higgs boson. Its virtual contribution (through quantum loop corrections) modify the predicted values for almost any observable.
To try a summary of the success of the standard electroweak model
![]() would imply to multiply several times
the content of this course. Let us only say that the theory works
dramatically well for our reality, in spite of the existence of
valid theoretical and structural reasons as the presence of all
the free parameters cited above to transcend the model in some
direction. Nevertheless, we have chosen to present a verification,
one of the first, which has a relaxing flavor at the time of the
lecture:
would imply to multiply several times
the content of this course. Let us only say that the theory works
dramatically well for our reality, in spite of the existence of
valid theoretical and structural reasons as the presence of all
the free parameters cited above to transcend the model in some
direction. Nevertheless, we have chosen to present a verification,
one of the first, which has a relaxing flavor at the time of the
lecture:
Part of the first page of the Review of Particle Properties
where the gauge bosons ![]() and
and ![]() , mediators of the weak
interactions, is also presented as Table 20.
, mediators of the weak
interactions, is also presented as Table 20.
Finally we include in Table 1 the usual set of physical observables together with their Standard Model predictions and their present and future experimental uncertainties.