The strong interactions among quarks and gluons are described by
Quantum Chromodynamics (QCD), the non-abelian gauge theory based
on the gauge group ![]() . Each quark flavour corresponds to a
colour triplet in the fundamental representation of
. Each quark flavour corresponds to a
colour triplet in the fundamental representation of ![]() and
the gauge fields needed to maintain the gauge symmetry, the
gluons, are in the adjoint representation of dimension 8. Gauge
invariance, realized á la Wigner-Weyl, ensures that gluons are
massless. The QCD Lagrangian may be written as
and
the gauge fields needed to maintain the gauge symmetry, the
gluons, are in the adjoint representation of dimension 8. Gauge
invariance, realized á la Wigner-Weyl, ensures that gluons are
massless. The QCD Lagrangian may be written as
| (364) |
| (365) |
Like in Quantum Electrodynamics (QED), the procedure employed to deal consistently with the divergences that occur in the computation of strong interactions beyond the tree level, shows that the actual strong coupling depends on the energy scale of the process. But in opposition to QED, this renormalized strong coupling is small at high energy (momentum), going to zero logarithmically. QCD has the property of asymptotic freedom. Consequently, in this regime perturbation theory is valid and tests against experimental data can be performed in terms of hadrons. Figure 21 summarize the basic QCD perturbative processes appearing in different circumstances.
Experiments with ![]() colliders provide clean results for
QCD tests. Recently, a huge amount of experimental data came from
the HERA electron-proton collider and also from the Tevatron at
Fermilab. In both cases, there is a hadronic remnant that make the
analysis a little more involved. All this experimental evidence
support the existence of quarks being colour triplets of spin
colliders provide clean results for
QCD tests. Recently, a huge amount of experimental data came from
the HERA electron-proton collider and also from the Tevatron at
Fermilab. In both cases, there is a hadronic remnant that make the
analysis a little more involved. All this experimental evidence
support the existence of quarks being colour triplets of spin
![]() and of gluons being vector octets. Moreover, the presence of
the QCD coupling has manifested itself in different measurements,
as well as the above mentioned property of asymptotic freedom.
This information comes mainly from the study of the so called two-
and three-jets events mentioned in the phenomenological
introduction.
and of gluons being vector octets. Moreover, the presence of
the QCD coupling has manifested itself in different measurements,
as well as the above mentioned property of asymptotic freedom.
This information comes mainly from the study of the so called two-
and three-jets events mentioned in the phenomenological
introduction.
When a given process needs a higher order in perturbation theory
to be known, it is necessary to compute not only the renormalized
strong coupling constant but also the appropriate corrections to
the relevant cross-sections. As is usual in Quantum Field Theory,
a regularization-renormalization procedure is in order, just to
absorb divergences into the definition of physical quantities.
This prescription requires the introduction of a new scale ![]() ,
fixing the renormalization point, and all renormalized quantities
begin to depend on it. Nevertheless, different prescriptions must
end with the same predictions for observables.
,
fixing the renormalization point, and all renormalized quantities
begin to depend on it. Nevertheless, different prescriptions must
end with the same predictions for observables.
In order to illustrate how the general procedure works, ending
with the Renormalization Group equations that guarantee that
physical observables do not depend on the scale ![]() , let us show
what happens with Green functions. Just to remember the procedure,
let us begin with a single particle irreducible Green function
, let us show
what happens with Green functions. Just to remember the procedure,
let us begin with a single particle irreducible Green function
![]() . In general, to control divergences, one has to introduce
an ultra-violet cut-off
. In general, to control divergences, one has to introduce
an ultra-violet cut-off ![]() , or the equivalent dimensional
regularization parameter, in the loop momentum integral defining
the
, or the equivalent dimensional
regularization parameter, in the loop momentum integral defining
the ![]() . In a renormalizable theory, as QCD is, a
renormalized Green function is defined as
. In a renormalizable theory, as QCD is, a
renormalized Green function is defined as
| (366) |
| (367) |
If there is only one large momentum scale ![]() , or
, or ![]() as it is
standard to quote, as it is the case here, one can express all
as it is
standard to quote, as it is the case here, one can express all
![]() in terms of a fixed fraction
in terms of a fixed fraction ![]() of
of ![]() . Then, defining
the so called evolution variable
. Then, defining
the so called evolution variable
| (368) |
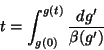
![\begin{displaymath}
\Gamma(t,g(0),x_i) = \Gamma(0,g(t),x_i) exp \left[
\int^...
...prime} \frac{\gamma(g^{\prime})}
{\beta(g^{\prime})} \right]
\end{displaymath}](img802.gif)
| (369) |
| (370) |
| (371) |
It is clear that the solution of the differential equation for
![]() introduces a constant, called
introduces a constant, called ![]() , which
has to be fixed by using experimental data. The resulting
, which
has to be fixed by using experimental data. The resulting
![]() can be written as
can be written as
This expression for the running coupling shows clearly the
property of asymptotic freedom of QCD, i.e., the coupling vanishes
when the scale becomes asymptotic, namely
![]() . Consequently, in this momentum regime, perturbation
theory is valid.
. Consequently, in this momentum regime, perturbation
theory is valid.
A very clear quantitative test of perturbative QCD is provided by
the measurement of ![]() in different processes at different
scales
in different processes at different
scales ![]() . In Figure 22 there is a summary of the
various determinations of
. In Figure 22 there is a summary of the
various determinations of ![]() .
.
The present world average for the coupling at the ![]() mass is
mass is
This small paragraph devoted to the factor ![]() of
of ![]() which
represents the Standard Model of the Electroweak and Strong Interactions
is only worth as a preface to the corresponding course on QCD.
which
represents the Standard Model of the Electroweak and Strong Interactions
is only worth as a preface to the corresponding course on QCD.