


Next: An Objective: the Weak
Up: The Standard Model of
Previous: The Idea and the
The language of particle physics is the Quantum Field Theory. In
this formalism to each fundamental excitation corresponds a quantum
field
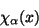 |
(13) |
where 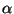 indicates the necessary group of indeces to characterize the
field. It is also possible to easily add eventual symmetries
introducing invariant Lagrangians (or Actions) in front of a given
symmetry operations. That is to say, functions
which do not change when the fields are subjected to the operation of
a
indicates the necessary group of indeces to characterize the
field. It is also possible to easily add eventual symmetries
introducing invariant Lagrangians (or Actions) in front of a given
symmetry operations. That is to say, functions
which do not change when the fields are subjected to the operation of
a  group of symmetry transformations. In this case, the field
group of symmetry transformations. In this case, the field
 is
a member of an irreducible multiplet, that is to say, under the
operation
is
a member of an irreducible multiplet, that is to say, under the
operation 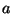 of the
of the  group
group
 |
(14) |
where
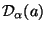 is the corresponding representation of
is the corresponding representation of  . So, if
. So, if
 |
(15) |
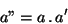 |
(16) |
then
 |
(17) |
These
operations imply, seen from the Hilbert space, the existence of a
unitary operator 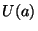 for the operation
for the operation 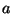 , so it satisfies
, so it satisfies
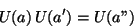 |
(18) |
and acting on the field verifies
the relation
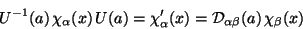 |
(19) |
which indicates that
If we are dealing with continuous transformations, the study can
be restricted to the infinitesimal transformations of the form
 |
(20) |
where 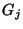 are the generators of the group algebra. As unitary groups
are concerned,
are the generators of the group algebra. As unitary groups
are concerned, 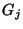 are hermitic operators. The Lie algebra of the
group is defined by
are hermitic operators. The Lie algebra of the
group is defined by
![\begin{displaymath}[G_{i},G_{j}]= i C_{ijk} G_{k}
\end{displaymath}](img71.gif) |
(21) |
with  the structure constants of the group.
The corresponding representations
the structure constants of the group.
The corresponding representations 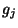 of the generators
of the generators 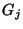 are
defined by
are
defined by
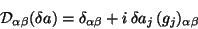 |
(22) |
with the obvious property
![\begin{displaymath}[g_{i},g_{j}]= i C_{ijk} g_{k}
\end{displaymath}](img75.gif) |
(23) |
Being
 an irreducible tensorial operator, one
can immediately write the relation
an irreducible tensorial operator, one
can immediately write the relation
![\begin{displaymath}[G_{j},\chi_{\alpha}(x)]=
- (g_{i})_{\alpha\beta} \chi_{\beta}(x)
\end{displaymath}](img76.gif) |
(24) |
A theory is invariant under a group  if after the symmetry
transformation it is verified that
if after the symmetry
transformation it is verified that
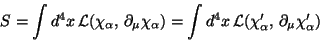 |
(25) |
that is to say
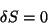 |
(26) |
The invariance leads to the presence, via Noether theorem, of a
conserved current.
As the field variation is written
 |
(27) |
it results
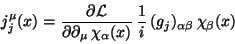 |
(28) |
with the property
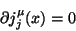 |
(29) |
which also implies that the generator (the charge)
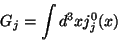 |
(30) |
is independent of the time, that
is to say
![\begin{displaymath}[H,G_{j}]= 0
\end{displaymath}](img83.gif) |
(31) |
which is other way of expressing
the invariance of the theory under the group  .
Let us study now the states. A state of one particle is written:
.
Let us study now the states. A state of one particle is written:
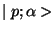 with
with
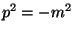 .
.
If and only if the vacuum is  invariant, that is, if and only if
invariant, that is, if and only if
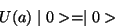 |
(32) |
that is
 |
(33) |
then the states of a particle associated with the field
 are
analogously transformed to
are
analogously transformed to
 Let us remember the reduction scheme LSZ
Let us remember the reduction scheme LSZ
 |
(34) |
and then
that is to say
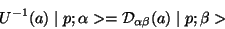 |
(38) |
This property implies that all the states of the multiplete
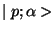 have
the same mass:
If
have
the same mass:
If
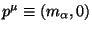 , the rest state
, the rest state
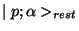 is defined through
is defined through
 |
(39) |
On the other hand, due to the invariance under  it is possible to
write
it is possible to
write
![\begin{displaymath}[H,U^{-1}(a)]= 0
\end{displaymath}](img97.gif) |
(40) |
then
which taking into account the arbitrariness of  shows that
shows that
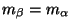
We conclude that the particles associated with fields which
irreducibly transform under a group  have the same mass. This
is the Wigner-Weyl realization of the symmetry.
As an example we remember the isospin symmetry which implies
have the same mass. This
is the Wigner-Weyl realization of the symmetry.
As an example we remember the isospin symmetry which implies
 when electromagnetism is absent.
when electromagnetism is absent.
What happens when the vaccum is not  invariant, that is to say
when
invariant, that is to say
when
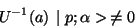 |
(43) |
Then the fundamental state is not unique: the fundamental state is
degenerate. As a consequence the symmetry in this case does not
imply multipletes of particles of the same mass. That is
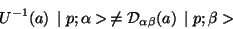 |
(44) |
even if
![\begin{displaymath}[H,G_{j}]= 0
\end{displaymath}](img83.gif) |
(45) |
In this case we
speak of a Nambu-Goldstone realization of the symmetry and
the following theorem is verified:
If a theory is  invariant and the vaccum state (fundamental) is
not
invariant and the vaccum state (fundamental) is
not  invariant then there appear null mass excitations called
Goldstone bosons. Let us see why.
The relation
invariant then there appear null mass excitations called
Goldstone bosons. Let us see why.
The relation
![\begin{displaymath}[G_{j},\chi_{\alpha}(x)]= - (g_{j})_{\alpha\beta} \chi_{\beta}(x)
\end{displaymath}](img106.gif) |
(46) |
leads to
![\begin{displaymath}
<0\mid [G_{j},\chi_{\alpha}(x)] \mid 0> = - (g_{j})_{\alpha\beta}
<0\mid \chi_{\beta}(x) \mid 0>
\end{displaymath}](img107.gif) |
(47) |
and as the realization of the symmetry is
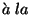 Nambu-Goldstone
Nambu-Goldstone
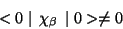 |
(48) |
Besides, we can explicitly write
Introducing now intermediate states  and the traslation
and the traslation
 |
(50) |
results
On the other hand
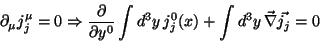 |
(53) |
and then
If we now observe in I the terms  with
with 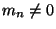 we see that they lead
to factors
we see that they lead
to factors
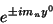 |
(55) |
which imply an explicit dependence in  not allowed and therefore it
must be
not allowed and therefore it
must be
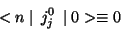 |
(56) |
Besides, the state
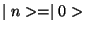 makes explicitly
makes explicitly 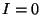 .
We conclude then that there must be some state
.
We conclude then that there must be some state
 so that
so that
 |
(57) |
independent from  with the property
with the property
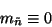 |
(58) |
which is precisely the state that is called Goldstone boson.
The previous development shows us that for each generator 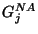 that does not annihilate the vaccum there appears a Goldstone boson. In other words,
the action of each
that does not annihilate the vaccum there appears a Goldstone boson. In other words,
the action of each 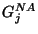 on
on 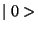 makes appear one state
makes appear one state 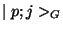 with
with  .
Summarizing a bit more formally:
If a system presents a continuous symmetry related to a group
.
Summarizing a bit more formally:
If a system presents a continuous symmetry related to a group  of
of 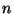 parameters and the solutions exhibit, on the contrary, a symmetry
associated to a subgroup of
parameters and the solutions exhibit, on the contrary, a symmetry
associated to a subgroup of  parameters, then there appear in the
theory
parameters, then there appear in the
theory 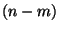 scalar (or pseudoscalar) partcles without mass: my bosons,
as Goldstone would say.
scalar (or pseudoscalar) partcles without mass: my bosons,
as Goldstone would say.



Next: An Objective: the Weak
Up: The Standard Model of
Previous: The Idea and the
root
2001-01-22
![]() an irreducible tensorial operator, one
can immediately write the relation
an irreducible tensorial operator, one
can immediately write the relation
![]() if after the symmetry
transformation it is verified that
if after the symmetry
transformation it is verified that
![]() invariant, that is, if and only if
invariant, that is, if and only if
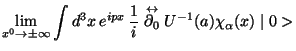
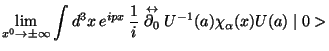

![]() have
the same mass:
If
have
the same mass:
If
![]() , the rest state
, the rest state
![]() is defined through
is defined through
![]() have the same mass. This
is the Wigner-Weyl realization of the symmetry.
As an example we remember the isospin symmetry which implies
have the same mass. This
is the Wigner-Weyl realization of the symmetry.
As an example we remember the isospin symmetry which implies
![]() when electromagnetism is absent.
when electromagnetism is absent.
![]() invariant, that is to say
when
invariant, that is to say
when

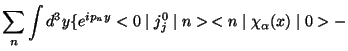
![$\displaystyle \frac{\partial}{\partial y^{0}}\int d^{3}y<0\mid [
j_{j}^{0}(y),\chi_{\alpha}(x)]\mid 0>$](img121.gif)
![$\displaystyle -\int d^{3}y <0\mid
[\vec{\nabla}\vec{j_{j}},\chi_{\alpha}(x)]\mid 0>$](img122.gif)
![$\displaystyle -\int_{S}d\vec{\sigma}<0\mid [\vec{j}_{j},\chi_{\alpha}]\mid 0>$](img123.gif)
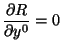
![]() with
with ![]() we see that they lead
to factors
we see that they lead
to factors
![]() makes explicitly
makes explicitly ![]() .
We conclude then that there must be some state
.
We conclude then that there must be some state
![]() so that
so that