


Next: Radiation and luminous matter
Up: THE DARK MATTER OF
Previous: THE DARK MATTER OF
We wish to discuss the inventory of the mass (energy) of the universe.
Assuming that for large scale the universe is homogeneous, we may use the
Robertson-Walker metric
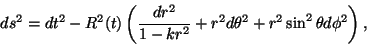 |
(1) |
where 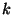 is a constant. It may be seen that the 3-dimensional space is closed,
open or flat for
is a constant. It may be seen that the 3-dimensional space is closed,
open or flat for 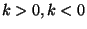 , or
, or 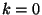 , respectively.
The Einstein equation relates the curvature of the metric to the
energy-momentum tensor through the Newton constant. For a perfect fluid,
characterized by energy density,
, respectively.
The Einstein equation relates the curvature of the metric to the
energy-momentum tensor through the Newton constant. For a perfect fluid,
characterized by energy density, 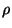 and pressure
and pressure 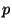 , the energy-momentum tensor is
, the energy-momentum tensor is
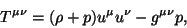 |
(2) |
where 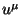 is the covariant velocity and
is the covariant velocity and
 diagonal tensor.
diagonal tensor.
The Einstein equation takes, therefore, the form of the Friedmann ones
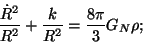 |
(3) |
 |
(4) |
The Hubble parameter is 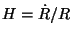 . Its value today is expressed in terms
of a constant
. Its value today is expressed in terms
of a constant  as
as
 |
(5) |
and the critical density is that which comes from Eq.(3) for 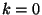 ,
i.e.,
,
i.e.,
 |
(6) |
Since
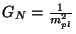 with the Planck mass
with the Planck mass
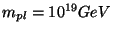 using
the equalities of the Appendix
using
the equalities of the Appendix
 |
(7) |
One important experimental result is the determination of the present value
of the Hubble constant which confirms that the universe is still expanding.
All current data are consistent with(2)
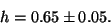 |
(8) |
According to Eq.(3) if the actual universe density is larger, equal or
smaller than the critical value of Eqs.(7, 8), the universe is closed, flat
or open respectively.



Next: Radiation and luminous matter
Up: THE DARK MATTER OF
Previous: THE DARK MATTER OF
root
2001-01-16
![]() . Its value today is expressed in terms
of a constant
. Its value today is expressed in terms
of a constant ![]() as
as
![]() with the Planck mass
with the Planck mass
![]() using
the equalities of the Appendix
using
the equalities of the Appendix