


Next: Dark baryonic matter
Up: THE DARK MATTER OF
Previous: Expanding universe
One contribution that can be easily estimated is that of the cosmic
background radiation (CBR) discovered in 1964 by Penzias and Wilson which
has been extremely well evaluated by the COBE satellite(3) as a black body
radiation of
 . From the Stefan-Boltzmann law and using
the Appendix
. From the Stefan-Boltzmann law and using
the Appendix
 |
(9) |
which corresponds to 400 photons per 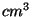 and is much smaller than the critical
density. Of course, since the decrease of
and is much smaller than the critical
density. Of course, since the decrease of  is faster with the universe
expansion than that of nonrelativistic matter
is faster with the universe
expansion than that of nonrelativistic matter
 |
(10) |
radiation must have dominated in the past.
It is usual to refer the different contributions of density to the critical
value so that at present from Eqs.(9) and (7)
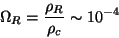 |
(11) |
The next obvious contribution to density is that of luminous matter. This is
evaluated summing over all the masses 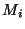 in a volume
in a volume  using a typical
mass to luminosity ratio
using a typical
mass to luminosity ratio
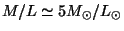 related to that
of sun.
related to that
of sun.
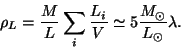 |
(12) |
From the measures of fluxes coming from bright regions of galaxies,
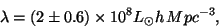 |
(13) |
where the  factor comes because the distances are calculated through the
Hubble law which gives the redshift
factor comes because the distances are calculated through the
Hubble law which gives the redshift
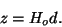 |
(14) |
Inserting the mass of the sun 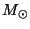 into Eq.(12) one obtains
into Eq.(12) one obtains
 |
(15) |
which again gives a small fraction of the critical density
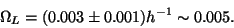 |
(16) |



Next: Dark baryonic matter
Up: THE DARK MATTER OF
Previous: Expanding universe
root
2001-01-16
![]() . From the Stefan-Boltzmann law and using
the Appendix
. From the Stefan-Boltzmann law and using
the Appendix
![]() in a volume
in a volume ![]() using a typical
mass to luminosity ratio
using a typical
mass to luminosity ratio
![]() related to that
of sun.
related to that
of sun.
![]() into Eq.(12) one obtains
into Eq.(12) one obtains