- ...)

- Actually, W is a section of a line bundle [33].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...,
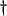
- From this section on, we will depart from the
conventions of the previous sections about the definitions of
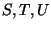 ,
the only change is to make
,
the only change is to make
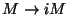 for
for 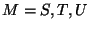 then
the axionic component is now the imaginary component of the complex field and
the compactification size is the real component of
then
the axionic component is now the imaginary component of the complex field and
the compactification size is the real component of 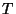 . The reason for this change is to have consistency with the standard supergravity conventions.
In particular, the
. The reason for this change is to have consistency with the standard supergravity conventions.
In particular, the
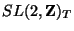 duality is now the transfoamtion
duality is now the transfoamtion
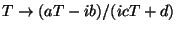 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... by
- The physical Yukawa couplings depend also on the Kähler potential,
see for instance [45].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
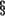
- Both of the last two statements have been recently
modified at the non-perturbative level,
by the studies of strong-weak coupling duality
symmetries (for a recent review see [104] ).
In particular there is some evidence for the
existence of an 11D theory from which all the different strings
could emerge. There is also evidence for the appearance
of nonperturbative gauge groups that can raise the rank beyond
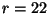 [55].
[55].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
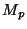
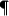
- This result will be drastically changed in the
brane-world scenario later where the string scale can be as small as 1
TeV
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...dsmac,bd.
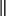
- This last claim depends on some CFT assumptions
[58] or that the breaking of supersymetry comes from an
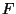 -term
[57].
There could be
counterexamples evading the assumptions.
-term
[57].
There could be
counterexamples evading the assumptions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... scale.
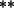
- For type I strings
the gravitational and gauge couplings are independent, so
we have the freedom to adjust the unification scale with experiment
as in usual GUTs
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... have
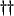
- The classical field
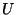 defined here has no relation with the moduli fields
defined here has no relation with the moduli fields 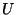 of the previous sections.
of the previous sections.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 3)
- Notice that the scalar potential blows up at large radius which is weak
sigma-model coupling. This is anti-intuitive, since we would have expected
the potential to vanish at weak coupling. A way to understand this is to realize that
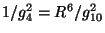 that
means that for large
that
means that for large 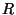 and fixed
and fixed 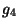 , the
original 10D string coupling becomes large, so the potential is blowing-up at strong string coupling
from the 10D point of view (we thank J. Polchinski and S.-J. Rey
for explaining this point).
, the
original 10D string coupling becomes large, so the potential is blowing-up at strong string coupling
from the 10D point of view (we thank J. Polchinski and S.-J. Rey
for explaining this point).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.