


Next: Gaugino Condensation
Up: SUPERSTRING PHENOMENOLOGY AND THE
Previous: Loop Corrections
Let us in this section recapitulate what we can say about string models
which is independent of the model.
This is the closest we can get to string predictions and
help us in approaching general questions, differentiating the
generic issues from those of a particular model.
Since the full nonperturbative formulation of string theory is not yet
available, we have to content ourselves mostly with
predictions of string perturbation theory, assuming that
the corresponding string model is given buy a CFT.
- (i)
First, as it was mentioned in the introduction, 4D string models
predict the existence of gravity and gauge interactions.
This is a point that cannot be overemphasized since it is the
first theory that makes those fundamental predictions for interactions
we experience in the every day life.
The dimension of spacetime is dynamical and
 raising the
hope that eventually we could explain if a 4D spacetime
is in some way special, although at present, the signature of spacetime is fixed in string theory as it is in QFT. Also
the rank of the gauge group is bounded
raising the
hope that eventually we could explain if a 4D spacetime
is in some way special, although at present, the signature of spacetime is fixed in string theory as it is in QFT. Also
the rank of the gauge group is bounded 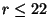
- (ii)There are other fields which
survive at low energies: charged matter fields, candidates to be basic blocks of matter but also the dilaton field
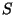 and other moduli
and other moduli
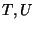 . We have to mention that, although as yet there
is no 4D model without moduli fields, there is not
a general theorem implying their existence. In that sense the dilaton is the most generic modulus field, with a flat potential
in perturbation theory.
. We have to mention that, although as yet there
is no 4D model without moduli fields, there is not
a general theorem implying their existence. In that sense the dilaton is the most generic modulus field, with a flat potential
in perturbation theory.
- (iii)There is only one arbitrary parameter
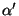 fixed to be close to the Planck scale
fixed to be close to the Planck scale
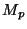
 . All other parameters
of the effective action are determined by expectation values of fields
such as the dilaton and the moduli. In particular the gauge coupling is
given at tree level by the vev of
. All other parameters
of the effective action are determined by expectation values of fields
such as the dilaton and the moduli. In particular the gauge coupling is
given at tree level by the vev of 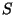 .
.
- (iv) The existence of spacetime supersymmetry is needed for consistency,
although
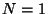 is selected for phenomenological reasons.
There is a general requirement for a CFT to lead to
is selected for phenomenological reasons.
There is a general requirement for a CFT to lead to 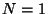 spacetime supersymmetry: It has to have
spacetime supersymmetry: It has to have  supersymmetry in the wordlsheet
(2D) (plus a quantization condition on the
charges of the
supersymmetry in the wordlsheet
(2D) (plus a quantization condition on the
charges of the 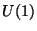 group mixing the two supersymmetries)
[56].
Furthermore, it is not possible to break supersymmetry
perturbatively nor in a continuous matter by the smooth variation of
a parameter
[57,58].
group mixing the two supersymmetries)
[56].
Furthermore, it is not possible to break supersymmetry
perturbatively nor in a continuous matter by the smooth variation of
a parameter
[57,58].

- (v) There are no global internal symmetries in 4D string
models
[58], besides the already mentioned Peccei-Quinn symmetry of
the
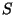 field and some accidental global symmetries
(like baryon and lepton numbers in the standard model).
This is a very strong result derived by showing that if there is
an internal symmetry, the properties of CFT's imply that there should
be a vector field in the spectrum with the properties of the gauge field of that
symmetry. This is consistent with similar claims about the
nonexistence of global symmetries in gravity, due for instance to
wormhole effects. This puts very strong constraints to string models
compared with standard field theory models.
field and some accidental global symmetries
(like baryon and lepton numbers in the standard model).
This is a very strong result derived by showing that if there is
an internal symmetry, the properties of CFT's imply that there should
be a vector field in the spectrum with the properties of the gauge field of that
symmetry. This is consistent with similar claims about the
nonexistence of global symmetries in gravity, due for instance to
wormhole effects. This puts very strong constraints to string models
compared with standard field theory models.
- (vi)There are generically some discrete symmetries
in string models. Some infinite dimensional
such as
 -duality and others finite dimensional as those inherited from the point
group of orbifold constructions, which are seen as
discrete gauge symmetries. These can in principle be useful for
model building, hierarchy of masses etc. There are however some couplings
that vanish in string theory and cannot be explained in terms of symmetries of the effective 4D theory, these are called `string miracles'
since from the 4D point of view they seem to break the criterium for naturalness [59].
As we saw in the previous section,
-duality and others finite dimensional as those inherited from the point
group of orbifold constructions, which are seen as
discrete gauge symmetries. These can in principle be useful for
model building, hierarchy of masses etc. There are however some couplings
that vanish in string theory and cannot be explained in terms of symmetries of the effective 4D theory, these are called `string miracles'
since from the 4D point of view they seem to break the criterium for naturalness [59].
As we saw in the previous section,  -duality symmetries restrict
very much the form of the effective action and quantities such as
Yukawa couplings have to be modular forms of a given duality group.
These symmetries are valid to all orders in string perturbation theory
and are thought to be also preserved by nonperturbative effects.
Matter fields
-duality symmetries restrict
very much the form of the effective action and quantities such as
Yukawa couplings have to be modular forms of a given duality group.
These symmetries are valid to all orders in string perturbation theory
and are thought to be also preserved by nonperturbative effects.
Matter fields 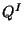 are assigned special quantum numbers,
the modular weights
are assigned special quantum numbers,
the modular weights  , according to their transformation properties under the duality group. For a
, according to their transformation properties under the duality group. For a
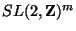 group for instance we have:
group for instance we have:
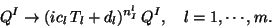 |
(33) |
Since fermions transform nontrivially under these symmetries, there
may be `duality anomalies' which have to be cancelled for consistency.
This imposes strong constraints on the possible spectrum of the
corresponding string model (which has to satisfy
 constant). For instance, using this, it can be shown that
it is impossible to obtain the minimal supersymmetric standard
model spectrum from any
constant). For instance, using this, it can be shown that
it is impossible to obtain the minimal supersymmetric standard
model spectrum from any 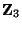 or
or 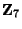 orbifold models
[60].
Anomaly cancellation also implies that the dilaton
orbifold models
[60].
Anomaly cancellation also implies that the dilaton 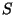 has
to transform nontrivially under
has
to transform nontrivially under  -duality, for factorized orbifolds:
-duality, for factorized orbifolds:
 |
(34) |
- (vii)
There is unification without the need of a GUT. If
the gauge group is a direct product of several groups we have
for the heterotic string
[61]:
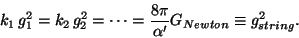 |
(35) |
Where 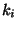 are special stringy constants known as the Kac-Moody levels of the corresponding
gauge groups (for the standard model groups it is usually assumed that
are special stringy constants known as the Kac-Moody levels of the corresponding
gauge groups (for the standard model groups it is usually assumed that
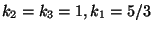 ).
We can see there is a difference with standard GUTs in field theory
for which we compute the unification scale by finding the
point where the different string couplings meet.
In heterotic string theory, the unification scale is given in terms of the
string coupling
).
We can see there is a difference with standard GUTs in field theory
for which we compute the unification scale by finding the
point where the different string couplings meet.
In heterotic string theory, the unification scale is given in terms of the
string coupling 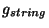 and the
Planck scale.
and the
Planck scale. More precisely:
More precisely:
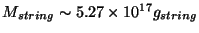 Gev.
For
Gev.
For
 this shows a discrepancy with the
`observed' value of the unification scale given by the
experiments
this shows a discrepancy with the
`observed' value of the unification scale given by the
experiments
 GeV. Also
the Weinberg angle gives
GeV. Also
the Weinberg angle gives
 differing from the
experimental value of
differing from the
experimental value of
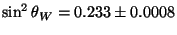 .
Therefore the string `predictions' are
very close to the experimental value, which is encouraging, but
differ by several standard deviations from it. This is the
string unification problem. The situation looks much better
for simple GUT's which have good agreement with experiment.
Several ideas have been proposed to cure this problem, including
large values of threshold corrections, intermediate scales, extra
particles, changing the values of Kac-Moody levels etc
[62], with
no compelling solution yet (for recent discussions of this
issue see for example [63] and the review of K. Dienes in ref. [5].).
Recently, a strong coupling solution of this problem was proposed which leads to a lower bound on Newton's constant, closed to the observed one [107].
.
Therefore the string `predictions' are
very close to the experimental value, which is encouraging, but
differ by several standard deviations from it. This is the
string unification problem. The situation looks much better
for simple GUT's which have good agreement with experiment.
Several ideas have been proposed to cure this problem, including
large values of threshold corrections, intermediate scales, extra
particles, changing the values of Kac-Moody levels etc
[62], with
no compelling solution yet (for recent discussions of this
issue see for example [63] and the review of K. Dienes in ref. [5].).
Recently, a strong coupling solution of this problem was proposed which leads to a lower bound on Newton's constant, closed to the observed one [107].
- (viii) Most of the models have Kac-Moody level
 and therefore cannot have
adjoint representation particles. In order to have GUTs from strings,
higher level models are then needed
[65]. These can be constructed from
level-one models, for instance the breaking of
and therefore cannot have
adjoint representation particles. In order to have GUTs from strings,
higher level models are then needed
[65]. These can be constructed from
level-one models, for instance the breaking of 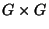 to
to
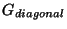 leads to a level-two model. Some three and four generation string- GUTs have been
explicitly constructed. General CFT relations show that
in order to implement the `missing partner'
and see-saw mechanisms in string GUTs we would need
Kac-Moody levels
leads to a level-two model. Some three and four generation string- GUTs have been
explicitly constructed. General CFT relations show that
in order to implement the `missing partner'
and see-saw mechanisms in string GUTs we would need
Kac-Moody levels 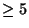 . Also, if the breaking to the standard model
by an adjoint is a flat direction then states transforming as
. Also, if the breaking to the standard model
by an adjoint is a flat direction then states transforming as
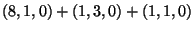 under
under
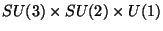 remain in the light spectrum
and could have low-energy implications.
remain in the light spectrum
and could have low-energy implications.
- (ix) There are usually fractionally charged particles in 4D string models [66].
In fact it can be shown that we cannot have simultaneously
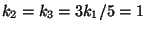 in the standard model and only integer charged
particles, because if that is the case the standard model
gauge group would be enhanced to a full level-one
in the standard model and only integer charged
particles, because if that is the case the standard model
gauge group would be enhanced to a full level-one
 [67]. This `problem' can be evaded in models where the
fractionally charged particles are heavy string states, it has
also been proposed that those particles could confine at intermediate energies and
be unobservable [68].
[67]. This `problem' can be evaded in models where the
fractionally charged particles are heavy string states, it has
also been proposed that those particles could confine at intermediate energies and
be unobservable [68].
- (x)Nonrenormalization theorems of the previous sections
are very strong and are model independent. We know the superpotential is exact at
tree-level and the
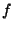 function is exact at one-loop. The Kähler
potential is however renormalized perturbatively.
These results imply that the lifting of flat directions and the breaking of
supersymmetry have to be achieved only at the string non-perturbative level (unless we do it by hand at tree-level [69] ).
function is exact at one-loop. The Kähler
potential is however renormalized perturbatively.
These results imply that the lifting of flat directions and the breaking of
supersymmetry have to be achieved only at the string non-perturbative level (unless we do it by hand at tree-level [69] ).
- (xi)
There are `anomalous'
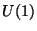 groups in most
of the models, but there is also a counterterm in the action cancelling the anomaly and generating a Fayet-Iliopoulos kind of term [70]:
groups in most
of the models, but there is also a counterterm in the action cancelling the anomaly and generating a Fayet-Iliopoulos kind of term [70]:
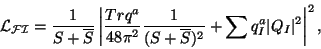 |
(36) |
where 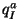 are the anomalous charges of the scalar fields
are the anomalous charges of the scalar fields 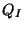 .
This term is responsable to break the would be anomalous group by fixing the
value of a combination of the matter fields
.
This term is responsable to break the would be anomalous group by fixing the
value of a combination of the matter fields 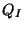 , breaking
the would be anomalous
, breaking
the would be anomalous 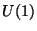 and usually other gauge groups, but not supersymmetry. A combination of the fields
and usually other gauge groups, but not supersymmetry. A combination of the fields 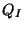 and the dilaton
and the dilaton 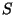 still remains massless and plays the role of the new dilaton field.
still remains massless and plays the role of the new dilaton field.
There are also further model independent results which refer to nonperturbative
string effects and will be discussed next.
Supersymmetry Breaking
0.4cm
In this chapter we will approach the problem of supersymmetry breaking in string theories in two complementary ways.
First we will discuss the favorite mechanism for low energy supersymmetry breaking, namely gaugino condensation, next we will
try to extract general information about the effects of
supersymmetry breaking, independent of the particular mechanism
that breaks, we will then discuss the general form of soft breaking terms expected in string models, independent of the breaking mechanism.
This is similar to the case of the standard model
where the Higgs sector can be treated as a black box but we can study the
low-energy theory below the symmetry breaking scale without
relying on the particular mechanism that broke the symmetry.
We will end up with general scenarios for the breaking
of supersymmetry, discussing in particular the very generic problem, known as
the `cosmological moduli problem'.
We have seen that in the efforts to extract a relation between string theory
and physics, there are two main problems, namely how
the large vacuum degeneracy is lifted and how
supersymmetry is broken at low energies.
These problems, when present at string tree level,
cannot be solved at any order in string perturbation
theory. Therefore the only
hope to solve them is nonperturbative physics.
This has a good and a bad side. The good side is that
nonperturbative effects represent the most natural way to
generate large hierarchies due to their exponential
suppression, this is precisely what is needed to obtain the
Weinberg-Salam scale from the fundamental string or Planck scale.
The bad side is that despite many efforts, we do not yet have
a nonperturbative formulation of string theory.
At the moment, the only concrete nonperturbative information
we can extract is from the purely field theoretical
nonperturbative
effects inside string theory (although a great amount of
progress has been made during the last year on nonperturbative string effects,
[104] ). Probably the simplest and
certainly the most studied of those effects is gaugino
condensation in a hidden sector of the gauge group, since it
has the potential of breaking supersymmetry as well as lifting
some of the flat directions, as we will presently discuss.
Subsections



Next: Gaugino Condensation
Up: SUPERSTRING PHENOMENOLOGY AND THE
Previous: Loop Corrections
root
2001-01-22