We have seen there is good understanding of some
of the tree-level couplings of 4D string models.
Also non-renormalization theorems guarantee that
the superpotential computed at tree-level is exact
at all orders in string perturbation theory.
This powerful result depends crucially on the fact that
the superpotential is a holomorphic function of the fields,
so if by the Peccei-Quinn symmetry cannot depend on the imaginary
part of the dilaton field ![]() , then it cannot depend neither
on the real part of
, then it cannot depend neither
on the real part of ![]() . This fact cannot be used for
the Kähler potential, which in general will be corrected
order by order in string perturbation theory.
This is then the least known part of any string theory
effective action.
On the other hand the gauge kinetic function
. This fact cannot be used for
the Kähler potential, which in general will be corrected
order by order in string perturbation theory.
This is then the least known part of any string theory
effective action.
On the other hand the gauge kinetic function ![]() is
also holomorhic and we know it exactly at the tree-level
(
is
also holomorhic and we know it exactly at the tree-level
(![]() ). Since this function determines the
gauge coupling itself, it is very interesting to
consider the loop corrections to
). Since this function determines the
gauge coupling itself, it is very interesting to
consider the loop corrections to ![]() .
.
During the past several years, explicit one-loop
corrections to ![]() have been computed, especially for
some orbifold models.
First it was shown that string loop diagrams reproduce the standard
running of the gauge couplings in field theory,
as expected. More interesting though, was to find the
finite corrections given by threshold effects which
include heavy string modes running in the loop.
These corrections will be functions of the moduli fields, such as the
geometric moduli
have been computed, especially for
some orbifold models.
First it was shown that string loop diagrams reproduce the standard
running of the gauge couplings in field theory,
as expected. More interesting though, was to find the
finite corrections given by threshold effects which
include heavy string modes running in the loop.
These corrections will be functions of the moduli fields, such as the
geometric moduli ![]() but also other moduli such as
continuous Wilson lines of orbifold models.
but also other moduli such as
continuous Wilson lines of orbifold models.
For factorized orbifold models,
the explicit dependence of the one-loop corrections
on the
![]() moduli fields takes the form [83]:
moduli fields takes the form [83]:
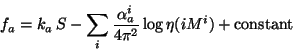 |
(29) |
| (30) |
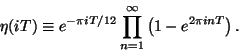 |
(31) |
The calculation of the string one-loop corrections to the gauge couplings is
better compared to the Lagrangian for the dilaton in a linear multiplet ![]() .
After performing the duality transformation it was found that those are not
only corrections to the function
.
After performing the duality transformation it was found that those are not
only corrections to the function ![]() but also to the Kähler potential
but also to the Kähler potential ![]() of
the form (for factorized orbifolds)[51]:
of
the form (for factorized orbifolds)[51]:
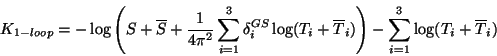 |
(32) |
The knowledge of loop corrections to ![]() is not only important for studying
questions of gauge coupling unification and supersymmetry breaking
by condensation of hidden sector gauge fermions.
It is also important because there is also a non-renormalization theorem
for
is not only important for studying
questions of gauge coupling unification and supersymmetry breaking
by condensation of hidden sector gauge fermions.
It is also important because there is also a non-renormalization theorem
for ![]() staying that there are no further
corrections to f beyond one-loop
[50]. This is again as in standard
supersymmetric theories [53]. The only thing to keep in mind is that
for
staying that there are no further
corrections to f beyond one-loop
[50]. This is again as in standard
supersymmetric theories [53]. The only thing to keep in mind is that
for ![]() it is important to state clearly that
we are working with the `Wilson' effective action rather than the 1PI
effective action.
In this case the gauge kinetic function is holomorphic
and does not get renormalized beyond one loop [53].
On the other hand, the 1PI gauge coupling is not holomorphic
and does get corrections from higher loops but, since it gives
the physical coupling, it is invariant under duality
symmetries.
it is important to state clearly that
we are working with the `Wilson' effective action rather than the 1PI
effective action.
In this case the gauge kinetic function is holomorphic
and does not get renormalized beyond one loop [53].
On the other hand, the 1PI gauge coupling is not holomorphic
and does get corrections from higher loops but, since it gives
the physical coupling, it is invariant under duality
symmetries.