


Next: Other Constructions
Up: SUPERSTRING PHENOMENOLOGY BEFORE 1995
Previous: Orbifold Compactifications
We saw that the orbifolds obtained from twisting the 6D tori
can give rise to chiral 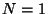 models in 4D. Orbifolds
are singular objects but they can be smoothed out by
blowing-up the singularities at the fixed points.
The resulting smooth manifold is a so-called Calabi-Yau
manifold [17]. Mathematically, these are 6D complex manifolds with
models in 4D. Orbifolds
are singular objects but they can be smoothed out by
blowing-up the singularities at the fixed points.
The resulting smooth manifold is a so-called Calabi-Yau
manifold [17]. Mathematically, these are 6D complex manifolds with 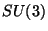 holonomy or equivalently vanishing first Chern class.
They were actually the first standard Kaluza-Klein compactification
considered in string theory, leading to chiral 4D models
and generically gauge group
holonomy or equivalently vanishing first Chern class.
They were actually the first standard Kaluza-Klein compactification
considered in string theory, leading to chiral 4D models
and generically gauge group 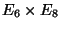 , with
, with 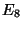 a
hidden gauge group.
a
hidden gauge group.
The drawback of compactifications on Calabi Yau manifolds
is that they are highly nontrivial spaces and
we cannot describe the strings on such manifolds, contrary to what
we did in the case of free theories such as tori and orbifolds.
In particular we can not compute explicitly the couplings
in the effective theory, except for the simplest renormalizable
Yukawa
couplings.
On the other hand, Calabi-Yau manifolds have been understood
much better during the past few years and have lead to some
beautiful and impressive results. In a way they are more general than orbifolds because an orbifold is only a particular
singular limit of a Calabi-Yau manifold. Also there are
other constructions of these manifolds which are
not related to orbifolds. They can be defined as
hypersurfaces in complex (weighted) projective spaces
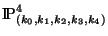 where
where 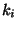 's are the weights
of the corresponding coordinates for which there is the
identification
's are the weights
of the corresponding coordinates for which there is the
identification
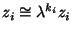 . The hypersurface is
defined as the vanishing locus of a polynomial of the
corresponding coordinates. For instance
the surface defined as:
. The hypersurface is
defined as the vanishing locus of a polynomial of the
corresponding coordinates. For instance
the surface defined as:
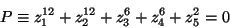 |
(13) |
defines a Calabi-Yau manifold with weights: .
The relation
.
The relation 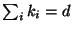 where
where 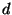 is the degree of the polynomial
ensures that the surface is a Calabi-Yau manifold. The manifold
is guaranteed to be smooth if both the polynomial
is the degree of the polynomial
ensures that the surface is a Calabi-Yau manifold. The manifold
is guaranteed to be smooth if both the polynomial 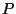 and its derivatives
do not vanish simultaneously.
Larger classes of manifolds can be
constructed by considering intersections of hypersurfaces in higher
dimensional projective spaces, the so-called complete intersection Calabi-Yau
manifolds (CICY). Actually, it is known in the mathematical literature, that
all Calabi-Yau spaces can be defined as
(intersection of) hypersurfaces in weighted projective spaces. Large numbers of these manifolds have been
classified, although the full classification is not complete.
The mathematical estimate is that there are of the order
of ten thousand Calabi-Yau manifolds. The corresponding string models
are of the type
and its derivatives
do not vanish simultaneously.
Larger classes of manifolds can be
constructed by considering intersections of hypersurfaces in higher
dimensional projective spaces, the so-called complete intersection Calabi-Yau
manifolds (CICY). Actually, it is known in the mathematical literature, that
all Calabi-Yau spaces can be defined as
(intersection of) hypersurfaces in weighted projective spaces. Large numbers of these manifolds have been
classified, although the full classification is not complete.
The mathematical estimate is that there are of the order
of ten thousand Calabi-Yau manifolds. The corresponding string models
are of the type 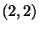 .
Some of the highlights of Calabi-Yau compactifications are
the following:
.
Some of the highlights of Calabi-Yau compactifications are
the following:
- (i) There are classes of moduli fields, generalizing
the fields
 and
and 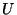 of the two-torus mentioned before.
The number of these fields is given by topological numbers
known as Hodge numbers
of the two-torus mentioned before.
The number of these fields is given by topological numbers
known as Hodge numbers
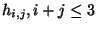 .
They correspond to the number of
complex harmonic forms that can be defined in the manifold
with
.
They correspond to the number of
complex harmonic forms that can be defined in the manifold
with 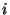 holomorphic indices and
holomorphic indices and  antiholomorphic
indices. Then the number of complex structure fields (U)
is given by
antiholomorphic
indices. Then the number of complex structure fields (U)
is given by 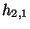 and the number of Kähler structure
fields (
and the number of Kähler structure
fields ( ) is given by
) is given by 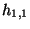 .
Many of the
.
Many of the 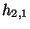 forms correspond to the coefficients of
different monomials which can be added to the defining polynomial
that still give rise to the same space, other forms correspond
to the blowing up of possible singularities. Many of the
forms correspond to the coefficients of
different monomials which can be added to the defining polynomial
that still give rise to the same space, other forms correspond
to the blowing up of possible singularities. Many of the 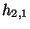 forms
correspond to polynomial deformations of the defining surface,
but others are related with the reparation of singularities.
For
Calabi-Yau manifolds we have
forms
correspond to polynomial deformations of the defining surface,
but others are related with the reparation of singularities.
For
Calabi-Yau manifolds we have 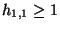 , therefore there is
always a special Kähler class deformation which can be thought
as the overall size of the corresponding manifold, it
is usually called, the Kähler form. All the other Hodge numbers
of Calabi-Yau manifolds are fixed (
, therefore there is
always a special Kähler class deformation which can be thought
as the overall size of the corresponding manifold, it
is usually called, the Kähler form. All the other Hodge numbers
of Calabi-Yau manifolds are fixed (
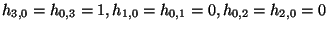 )
)
- (ii) The gauge group in 4D is
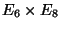 .
The matter fields transform as
.
The matter fields transform as 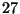 's or
's or
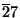 's
of
's
of 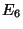 . The number of each is also given by the Hodge numbers
. The number of each is also given by the Hodge numbers
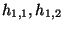 and the number of generations is then
topological:
and the number of generations is then
topological:
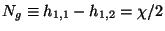 where
where
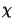 is the Euler number of the manifold. This is one of the
most appealing properties of these compactifications since they
imply that topology determines the number of quarks and leptons.
is the Euler number of the manifold. This is one of the
most appealing properties of these compactifications since they
imply that topology determines the number of quarks and leptons.
- (iii)Mirror symmetry [18]. Similar to the 2D toroidal compactifications,
it has been found that there is a mirror symmetry in Calabi-Yau
spaces that exchanges the moduli fields
 and
and 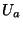
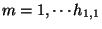 ,
,
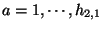 . This means that for every
Calabi-Yau manifold
. This means that for every
Calabi-Yau manifold  , there exists another
manifold
, there exists another
manifold 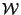 which has the complex and Kähler structure
fields exchanged, ie
which has the complex and Kähler structure
fields exchanged, ie
 and opposite Euler number
and opposite Euler number 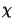 .
The mirror symmetry of the two-torus described previously,
is only a special example
on which the manifold is its own mirror.
Mirror symmetry is not only a nontrivial contribution
of string theory to modern mathematics, but it has very interesting
applications for computing effective Lagrangians as we will see in
the next section. It also relates the geometrical
modular symmetries associated to the
.
The mirror symmetry of the two-torus described previously,
is only a special example
on which the manifold is its own mirror.
Mirror symmetry is not only a nontrivial contribution
of string theory to modern mathematics, but it has very interesting
applications for computing effective Lagrangians as we will see in
the next section. It also relates the geometrical
modular symmetries associated to the 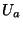 fields of the manifold
fields of the manifold  to generalized, stringy,
to generalized, stringy,  -duality symmetries for the mirror
-duality symmetries for the mirror
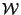 and viceversa (see for instance [19] ).
and viceversa (see for instance [19] ).
- (iv) Even though these string models are not completely understood in
terms of 2D CFTs, special points in the moduli space of a given
Calabi-Yau are CFTs, such as the orbifold compactifications mentioned
before. In fact some people believe that there is a one to one
correspondence
between string models with
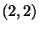 supersymmetry in the worldsheet and
Calabi-Yau manifolds. There is also a description of CFTs in terms of
effective Landau-Ginzburg Lagrangians which are intimately related
to Calabi-Yau compactifications as two phases of the same 2D theory
[20].
In particular the potential of that Landau-Ginzburg theory is
determined by the polynomial
supersymmetry in the worldsheet and
Calabi-Yau manifolds. There is also a description of CFTs in terms of
effective Landau-Ginzburg Lagrangians which are intimately related
to Calabi-Yau compactifications as two phases of the same 2D theory
[20].
In particular the potential of that Landau-Ginzburg theory is
determined by the polynomial 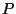 defining the Calabi-Yau hypersurface.
defining the Calabi-Yau hypersurface.
- (v) There are also few models with three generations that,
after the
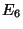 symmetry breaking, could lead to quasi-realistic
4D strings. One of these models was analyzed in some detail
[21].
Usually,
symmetry breaking, could lead to quasi-realistic
4D strings. One of these models was analyzed in some detail
[21].
Usually, 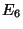 models also lead to the existence of extra
models also lead to the existence of extra 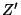 particles
of different kinds. They have been thoroughly studied because of
the potential experimental importance of detecting an
extra massive gauge boson (for a recent discussion see ref. [22] ).
particles
of different kinds. They have been thoroughly studied because of
the potential experimental importance of detecting an
extra massive gauge boson (for a recent discussion see ref. [22] ).
- (vi) Although most of the Calabi-Yau models studied so far
correspond to standard
embedding in the gauge degrees of freedom
(
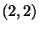 models), there is also
the possibility of constructing
models), there is also
the possibility of constructing  models by performing
different embeddings, similar to the orbifold case.
This increases substantially the number of string models
of this construction [23].
models by performing
different embeddings, similar to the orbifold case.
This increases substantially the number of string models
of this construction [23].



Next: Other Constructions
Up: SUPERSTRING PHENOMENOLOGY BEFORE 1995
Previous: Orbifold Compactifications
root
2001-01-22
![]() models in 4D. Orbifolds
are singular objects but they can be smoothed out by
blowing-up the singularities at the fixed points.
The resulting smooth manifold is a so-called Calabi-Yau
manifold [17]. Mathematically, these are 6D complex manifolds with
models in 4D. Orbifolds
are singular objects but they can be smoothed out by
blowing-up the singularities at the fixed points.
The resulting smooth manifold is a so-called Calabi-Yau
manifold [17]. Mathematically, these are 6D complex manifolds with ![]() holonomy or equivalently vanishing first Chern class.
They were actually the first standard Kaluza-Klein compactification
considered in string theory, leading to chiral 4D models
and generically gauge group
holonomy or equivalently vanishing first Chern class.
They were actually the first standard Kaluza-Klein compactification
considered in string theory, leading to chiral 4D models
and generically gauge group ![]() , with
, with ![]() a
hidden gauge group.
a
hidden gauge group.
![]() where
where ![]() 's are the weights
of the corresponding coordinates for which there is the
identification
's are the weights
of the corresponding coordinates for which there is the
identification
![]() . The hypersurface is
defined as the vanishing locus of a polynomial of the
corresponding coordinates. For instance
the surface defined as:
. The hypersurface is
defined as the vanishing locus of a polynomial of the
corresponding coordinates. For instance
the surface defined as: