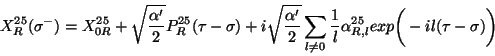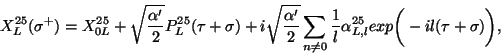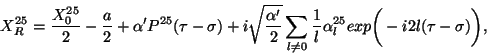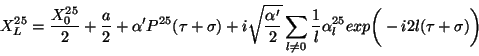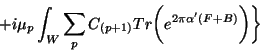Next: Non-perturbative String Theory
Up: T-duality, D-branes and Brane
Previous: T-duality, D-branes and Brane
D-branes are, despite of the dual fundamental degrees of freedom in string theory,
extremely interesting and useful tools to study nonperturbative properties of
string and field theories (for some reviews see [10,11]). Non-perturbative
properties of supersymmetric gauge theories can be better understanding as the
world-volume effective theory of some configurations of intersecting D-branes
(for a review see [14]). D-branes also are very important to connect gauge
theories with gravity. This is the starting point of the AdS/CFT correspondence
or Maldacena's conjecture. We don't review this interesting subject in this paper,
however the reader can consult the excellent review [15].
Roughly speaking D-branes are static solutions of string equations which satisfy
Dirichlet boundary conditions. That means that open strings can end on them.
To explain these objects we follow the traditional way, by using T-duality on
open strings we will see that Neumann conditions are turned out into the Dirichlet ones.
To motivate the subject we first consider T-duality in closed bosonic string theory.
truecm
T-duality in Closed Strings
The general solution of Eq. (4) in the conformal gauge can be written
as
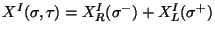 , where
, where
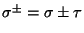 . Now, take one coordinate, say
. Now, take one coordinate, say 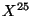 and compactify it on a
circle of radius
and compactify it on a
circle of radius  . Thus
we have that
. Thus
we have that 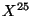 can be identified with
can be identified with
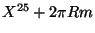 where
where 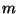 is called the
winding
number. The general solution for
is called the
winding
number. The general solution for 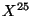 with the above compactification condition is
with the above compactification condition is
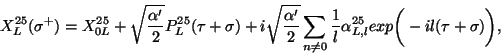 |
(38) |
where
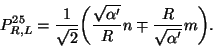 |
(39) |
Here 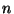 and
and 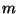 are integers representing the discrete momentum and the winding
number, respectively. The latter has not analogous in field theory.
While the canonical momentum is given by
are integers representing the discrete momentum and the winding
number, respectively. The latter has not analogous in field theory.
While the canonical momentum is given by
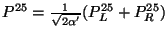 . Now, by the mass shell condition, the mass of the perturbative states
is given by
. Now, by the mass shell condition, the mass of the perturbative states
is given by
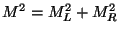 , with
, with
 |
(40) |
We can see that for all states with 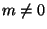 , as
, as  the mass
become infinity, while
the mass
become infinity, while 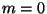 implies that the states take all values for
implies that the states take all values for 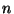 and form a
continuum. At the case when
and form a
continuum. At the case when  , for states with
, for states with 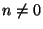 , mass
become infinity. However in the limit
, mass
become infinity. However in the limit  for
for 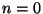 states with all
states with all
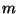 values produce a continuum in the spectrum. So, in this limit the compactified
dimension disappears. For this reason, we can say that the mass spectrum of the theories at radius
values produce a continuum in the spectrum. So, in this limit the compactified
dimension disappears. For this reason, we can say that the mass spectrum of the theories at radius
 and
and
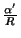 are identical when we interchange
are identical when we interchange
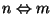 . This
symmetry is known as T-duality.
The importance of T-duality lies in the fact that the T-duality transformation is a parity
transformation acting on the left and right moving
degrees of freedom. It leaves invariant the left movers and changes the sign of the right movers
(see Eq. (39))
. This
symmetry is known as T-duality.
The importance of T-duality lies in the fact that the T-duality transformation is a parity
transformation acting on the left and right moving
degrees of freedom. It leaves invariant the left movers and changes the sign of the right movers
(see Eq. (39))
 |
(41) |
The action of T-duality transformation must leave invariant the whole theory
(at all order in perturbation theory). Thus, all kind of interacting states in certain theory
should correspond to those states belonging to the dual theory. In this context,
also the vertex operators are invariant. For instance the tachyonic vertex operators are
 |
(42) |
Under T-duality,
 and
and
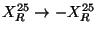 ; and from the general solution Eq. (38),
; and from the general solution Eq. (38),
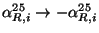 ,
,
 . Thus, T-duality
interchanges
. Thus, T-duality
interchanges
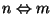 (Kaluza-Klein modes
(Kaluza-Klein modes
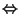 winding
number) and
winding
number) and
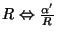 in closed string theory.
truecm
T-duality in Open Strings
Now, consider open strings with Neumann boundary conditions. Take again the
in closed string theory.
truecm
T-duality in Open Strings
Now, consider open strings with Neumann boundary conditions. Take again the
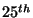 coordinate and compactify it on a circle of radius
coordinate and compactify it on a circle of radius  , but keeping Neumann
conditions. As in the case of closed string, center of mass momentum takes only discrete
values
, but keeping Neumann
conditions. As in the case of closed string, center of mass momentum takes only discrete
values
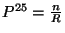 . While there is not analogous for the winding
number. So, when
. While there is not analogous for the winding
number. So, when  all states with nonzero momentum go to infinity
mass, and do not form a continuum. This behavior is similar as in field theory, but
now there is something new. The general solutions are
all states with nonzero momentum go to infinity
mass, and do not form a continuum. This behavior is similar as in field theory, but
now there is something new. The general solutions are
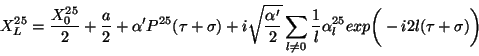 |
(43) |
where 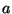 is a constant.
Thus,
is a constant.
Thus,
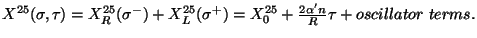 Taking the limit
Taking the limit  , only the
, only the  mode survives. Because of this,
the string seems to move in 25 spacetime dimensions. In other words, the strings vibrate in 24
transversal directions. T-duality provides a new T-dual coordinate defined by
mode survives. Because of this,
the string seems to move in 25 spacetime dimensions. In other words, the strings vibrate in 24
transversal directions. T-duality provides a new T-dual coordinate defined by
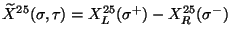 . Now, taking
. Now, taking
 we have
we have
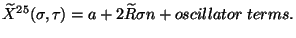 Using the boundary conditions at
Using the boundary conditions at 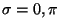 one has
one has
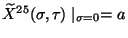 and
and
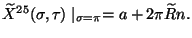 Thus, we started with an open bosonic string theory with Neumann boundary
conditions, and T-duality and a compactification on a circle in the
Thus, we started with an open bosonic string theory with Neumann boundary
conditions, and T-duality and a compactification on a circle in the 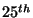 dimension, give us Dirichlet boundary conditions in such a coordinate. We can
visualize this saying that an open string has its endpoints fixed at a hyperplane
with 24 dimensions.
Strings with
dimension, give us Dirichlet boundary conditions in such a coordinate. We can
visualize this saying that an open string has its endpoints fixed at a hyperplane
with 24 dimensions.
Strings with 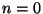 lie on a 24 dimensional plane space (D24-brane). Strings with
lie on a 24 dimensional plane space (D24-brane). Strings with
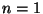 has one endpoint at a hyperplane and the other at a different hyperplane which
is separated from the first one by a factor equal to
has one endpoint at a hyperplane and the other at a different hyperplane which
is separated from the first one by a factor equal to
 , and so on. But
if we compactify
, and so on. But
if we compactify 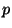 of the
of the  directions over a
directions over a 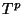 torus (
torus (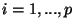 ). Thus, after
T-dualizing
them we have strings with endpoints fixed at hyperplane with
). Thus, after
T-dualizing
them we have strings with endpoints fixed at hyperplane with 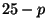 dimensions, the D
dimensions, the D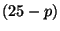 -brane.
Summarizing: the system of open strings moving freely in spacetime with
-brane.
Summarizing: the system of open strings moving freely in spacetime with 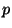 compactified
dimensions on
compactified
dimensions on 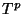 is equivalent, under T-duality, to strings whose enpoints are fixed at a
D
is equivalent, under T-duality, to strings whose enpoints are fixed at a
D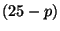 -brane i.e. obeying Neumann boundary conditions in the
-brane i.e. obeying Neumann boundary conditions in the  longitudinal
directions (
longitudinal
directions (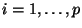 ) and Dirichlet ones in the transverse coordinates
) and Dirichlet ones in the transverse coordinates 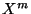 (
(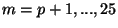 ).
The effect of T-dualizing a coordinate is to change the nature of the boundary conditions, from
Neumann to Dirichlet and vice versa. If one dualize a longitudinal coordinate this coordinate
will
satisfies the Dirichlet condition and a D
).
The effect of T-dualizing a coordinate is to change the nature of the boundary conditions, from
Neumann to Dirichlet and vice versa. If one dualize a longitudinal coordinate this coordinate
will
satisfies the Dirichlet condition and a D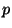 -brane becomes a D
-brane becomes a D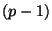 -brane. But if the
dualized coordinate is one of the transverse coordinates the D
-brane. But if the
dualized coordinate is one of the transverse coordinates the D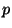 -brane becomes a
D
-brane becomes a
D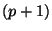 -brane.
T-duality also acts conversely. We can think to begin with
a closed string theory, and compactify it on to a circle in
the
-brane.
T-duality also acts conversely. We can think to begin with
a closed string theory, and compactify it on to a circle in
the 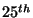 coordinate, and then by imposing Dirichlet conditions, obtain a
D-brane. This is precisely what occurs in Type II theory, a theory of closed strings.
truecm
Spectrum and Wilson Lines
Now, we will see how does emerges a gauge field on the D
coordinate, and then by imposing Dirichlet conditions, obtain a
D-brane. This is precisely what occurs in Type II theory, a theory of closed strings.
truecm
Spectrum and Wilson Lines
Now, we will see how does emerges a gauge field on the D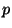 -brane world-volume. Again, for
the mass
shell condition for open bosonic strings and because T-duality
-brane world-volume. Again, for
the mass
shell condition for open bosonic strings and because T-duality
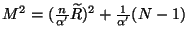 . The massless state
(
. The massless state
(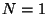 ,
, 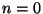 ) implies that the gauge boson
) implies that the gauge boson
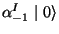 (
(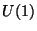 gauge boson) lies on the D24-brane world-volume. On the other hand,
gauge boson) lies on the D24-brane world-volume. On the other hand,
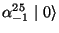 has a vev (vacuum expectation value) which describes
the position
has a vev (vacuum expectation value) which describes
the position
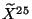 of the D-brane after T-dualizing. Thus, we can say
in general, there is a gauge theory
of the D-brane after T-dualizing. Thus, we can say
in general, there is a gauge theory 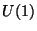 over the world volume of the D
over the world volume of the D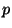 -brane.
Consider now an orientable open string. The endpoints of the string carry
charge under a non-Abelian gauge group. For Type II theories the gauge group is
-brane.
Consider now an orientable open string. The endpoints of the string carry
charge under a non-Abelian gauge group. For Type II theories the gauge group is
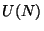 . One endpoint transforms under the fundamental
representation
. One endpoint transforms under the fundamental
representation 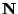 of
of 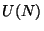 and the other one, under its complex conjugate representation
(the anti-fundamental one)
and the other one, under its complex conjugate representation
(the anti-fundamental one)  .
The ground state wave function is specified by the center of mass momentum and by
the charges of the endpoints. Thus implies the existence of a basis
.
The ground state wave function is specified by the center of mass momentum and by
the charges of the endpoints. Thus implies the existence of a basis
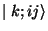 called Chan-Paton basis. States
called Chan-Paton basis. States
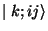 of the Chan-Paton basis are those
states which carry charge 1 under the
of the Chan-Paton basis are those
states which carry charge 1 under the 
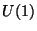 generator and
generator and 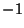 under the
under the

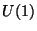 generator. So, we can decompose the wave function for ground state
as
generator. So, we can decompose the wave function for ground state
as
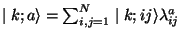 where
where
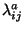 are
called Chan-Paton factors. From this, we see that it is possible to add degrees of freedom
to endpoints of the string, that are precisely the Chan-Paton factors.
This is consistent with the theory, because the Chan-Paton factors have a Hamiltonian
which do not posses dynamical structure. So, if one endpoint to the string is
prepared in a certain state, it always will remains the same. It can be deduced from
this, that
are
called Chan-Paton factors. From this, we see that it is possible to add degrees of freedom
to endpoints of the string, that are precisely the Chan-Paton factors.
This is consistent with the theory, because the Chan-Paton factors have a Hamiltonian
which do not posses dynamical structure. So, if one endpoint to the string is
prepared in a certain state, it always will remains the same. It can be deduced from
this, that
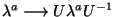 with
with 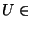
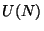 . Thus, the worldsheet
theory is
symmetric under
. Thus, the worldsheet
theory is
symmetric under 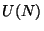 , and this global symmetry is a gauge symmetry in spacetime. So the
vector state at massless level
, and this global symmetry is a gauge symmetry in spacetime. So the
vector state at massless level
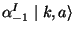 is a
is a 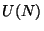 gauge boson.
When we have a gauge configuration with non trivial line integral around a
compactified dimension (i.e a circle), we said there is a Wilson line. In case of
open strings with gauge group
gauge boson.
When we have a gauge configuration with non trivial line integral around a
compactified dimension (i.e a circle), we said there is a Wilson line. In case of
open strings with gauge group 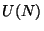 , a toroidal compactification of the
, a toroidal compactification of the 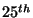 dimension on a circle of radius
dimension on a circle of radius  . If we choice a background field
. If we choice a background field 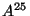 given
by
given
by
 a Wilson line
appears. Moreover, if
a Wilson line
appears. Moreover, if 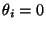 ,
, 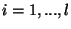 and
and
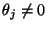 ,
,  then gauge group is broken:
then gauge group is broken:
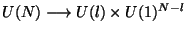 . It is
possible to deduce that
. It is
possible to deduce that  plays the role of a Higgs field.
Because string states with Chan-Paton quantum numbers
plays the role of a Higgs field.
Because string states with Chan-Paton quantum numbers
 have charges
have charges  under
under 
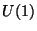 factor (and
factor (and 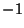 under
under 
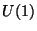 factor) and neutral with
all others; canonical momentum is given now by
factor) and neutral with
all others; canonical momentum is given now by
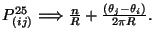 Returning to the mass shell condition it results,
Returning to the mass shell condition it results,
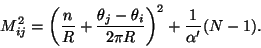 |
(44) |
Massless states (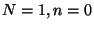 ) are those in where
) are those in where 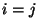 (diagonal terms) or for which
(diagonal terms) or for which

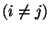 . Now, T-dualizing we have
. Now, T-dualizing we have
 Taking
Taking
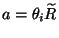 ,
,
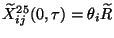 and
and
 This give us a set of
This give us a set of 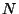 D-branes whose positions are given by
D-branes whose positions are given by
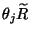 , and each set is separated from its initial positions
(
, and each set is separated from its initial positions
( ) by a factor equal to
) by a factor equal to
 .
Open strings with both endpoints on the same D-brane gives massless gauge bosons.
The set of
.
Open strings with both endpoints on the same D-brane gives massless gauge bosons.
The set of 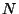 D-branes give us
D-branes give us  gauge group. An open string with one endpoint
in one D-brane, and the other endpoint in a different D-brane, yields a
massive state with
gauge group. An open string with one endpoint
in one D-brane, and the other endpoint in a different D-brane, yields a
massive state with
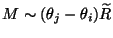 . Mass decreases when two
different D-branes approximate to each other, and are null when become the same.
When all D-branes take up the same position, the gauge group is enhanced from
. Mass decreases when two
different D-branes approximate to each other, and are null when become the same.
When all D-branes take up the same position, the gauge group is enhanced from  to
to
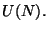 On the D-brane world-volume there are also scalar fields in the adjoint representation
of the gauge group
On the D-brane world-volume there are also scalar fields in the adjoint representation
of the gauge group 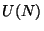 . The scalars parametrize the transverse positions of the D-brane in the
target space
. The scalars parametrize the transverse positions of the D-brane in the
target space 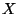 .
truecm
D-Brane Action
With the massless spectrum on the D-brane world-volume it is possible to construct a low
energy effective action. Open strings massless fields are interacting with the closed
strings massless spectrum from the NS-NS sector. Let
.
truecm
D-Brane Action
With the massless spectrum on the D-brane world-volume it is possible to construct a low
energy effective action. Open strings massless fields are interacting with the closed
strings massless spectrum from the NS-NS sector. Let 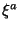 (with
(with
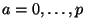 ) be the world-volume coordinates on
) be the world-volume coordinates on 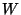 . The effective action is the gauge invariant
action well known as the Dirac-Born-Infeld (DBI)-action
. The effective action is the gauge invariant
action well known as the Dirac-Born-Infeld (DBI)-action
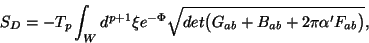 |
(45) |
where 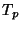 is the tension of the D-brane,
is the tension of the D-brane, 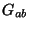 is the world-volume induced metric,
is the world-volume induced metric,
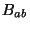 is the induced antisymmetric field,
is the induced antisymmetric field,  is the Abelian field strength on
is the Abelian field strength on
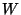 and
and 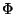 is the dilaton field.
For
is the dilaton field.
For 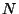 D-branes the massless fields turns out to be
D-branes the massless fields turns out to be 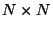 matrices and the
action turns out to be non-Abelian DBI-action (for a nice review about the Born-Infeld
action in string theory see [16])
matrices and the
action turns out to be non-Abelian DBI-action (for a nice review about the Born-Infeld
action in string theory see [16])
![\begin{displaymath}
S_D = - T_p \int_W d^{p+1} \xi e^{- \Phi} Tr\bigg(\sqrt{ de...
...2 \pi \alpha ' F_{ab}\big)} + O\big( [X^m,X^n]^2 \big) \bigg)
\end{displaymath}](img416.gif) |
(46) |
where
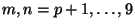 . The scalar fields
. The scalar fields 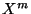 representing the transverse
positions become
representing the transverse
positions become 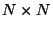 matrices and so, the spacetime become a noncommutative
spacetime. We will come back later to this interesting point.
truecm
Ramond-Ramond Charges
D-branes are coupled to Ramond-Ramond (RR) fields
matrices and so, the spacetime become a noncommutative
spacetime. We will come back later to this interesting point.
truecm
Ramond-Ramond Charges
D-branes are coupled to Ramond-Ramond (RR) fields  . The complete
effective action on the D-brane world-volume
. The complete
effective action on the D-brane world-volume 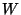 which taking into account this coupling
is
which taking into account this coupling
is
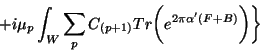 |
(47) |
where 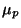 is the RR charge. RR charges can be computed by considering the anomalous
behavior of the action at intersections of D-branes. Thus RR charge is given
by
is the RR charge. RR charges can be computed by considering the anomalous
behavior of the action at intersections of D-branes. Thus RR charge is given
by
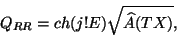 |
(48) |
where
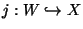 . Here
. Here 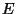 is the Chan-Paton bundle over
is the Chan-Paton bundle over 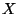 ,
,
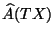 is the genus of the spacetime manifold
is the genus of the spacetime manifold 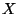 . This gives an ample evidence
that the RR charges take values not in a cohomology theory, but in fact, in a K-Theory.
This result was developed by Witten in Ref. [17] in the context of non-BPS brane
configurations worked out by Sen [18].
Finally, RR charges and RR fields do admit a classification in terms of topological
K-theory. The inclusion of a
. This gives an ample evidence
that the RR charges take values not in a cohomology theory, but in fact, in a K-Theory.
This result was developed by Witten in Ref. [17] in the context of non-BPS brane
configurations worked out by Sen [18].
Finally, RR charges and RR fields do admit a classification in terms of topological
K-theory. The inclusion of a 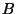 -field turns out the effective theory non-commutative and
a suitable generalization of the topological K-theory is needed. The right
generalization seems to be the K-Homology and the K-theory of
-field turns out the effective theory non-commutative and
a suitable generalization of the topological K-theory is needed. The right
generalization seems to be the K-Homology and the K-theory of 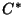 algebras
[19]. This subject is
right now under intensive investigation.
truecm
algebras
[19]. This subject is
right now under intensive investigation.
truecm



Next: Non-perturbative String Theory
Up: T-duality, D-branes and Brane
Previous: T-duality, D-branes and Brane
root
2001-01-15