


Next: Toroidal Compactification, -duality and
Up: STRINGS, BRANES AND DUALITY1
Previous: Calabi-Yau Compactifications in Perturbative
This section has the purpose of introducing basic ideas about T-duality in
closed and open string theory. The open string case leads in a natural way to
the definition of D-branes (for reviews of D-branes see [4,10,11]).
These objects are of extreme importance since
they are precisely the solitonic degrees of freedom which realize the strong-weak
coupling duality in superstring theory. This duality is also known as string S-duality.
T and S dualities relate the five perturbative superstring theories discussed previously
and their
compactifications in diverse dimensions. Moreover, the
strong coupling limit of HE and Type II string theory (and their compactifications) suggest that
there is an
eleven-dimensional theory which has the eleven-dimensional supergravity as low energy
limit. This prospect of theory is widely known as M-theory. The name come from the words: mystery,
magic, mother, etc. Compactifications to diverse lower dimensions than ten gives more evidence
of the existence of this theory. The fundamental degrees of freedom of this unified theory
are unknown, but macroscopically they include membranes and fivebranes. `Matrix Theory'
is an attempt to give the dof's of M-theory. The proposal is that these degrees of freedom
are the D0-branes. The worldvolume effective theory of a gas of 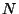 D0-branes is a
SU
D0-branes is a
SU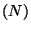 quantum mechanics. Large
quantum mechanics. Large 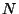 -limit reproduces the description of membranes and
fivebranes and some other results of eleven dimensional supergravity (for some reviews
the reader can consult [12,13]).
D-branes also, are very important tools to study the strong coupling of supersymmetric
theories in various dimensions. Different properties as chirality, dualities etc. are
encoded in the engineering of brane configurations. The moduli space of these susy
gauge theories is described by the Higgs and the Coulomb branches of the corresponding
brane configuration. Many field theory results are understanding in terms of a
geometrical language and many generalizations have been established motivated by the
brane engineering (more about this topic can be found in Ref. [14]).
Finally, the presence of branes leads to modify the prescription of Calabi-Yau or orbifold
compactifications and new non-perturbative are possible. In these sections we
will discuss some of these interesting topics.
truecm
-limit reproduces the description of membranes and
fivebranes and some other results of eleven dimensional supergravity (for some reviews
the reader can consult [12,13]).
D-branes also, are very important tools to study the strong coupling of supersymmetric
theories in various dimensions. Different properties as chirality, dualities etc. are
encoded in the engineering of brane configurations. The moduli space of these susy
gauge theories is described by the Higgs and the Coulomb branches of the corresponding
brane configuration. Many field theory results are understanding in terms of a
geometrical language and many generalizations have been established motivated by the
brane engineering (more about this topic can be found in Ref. [14]).
Finally, the presence of branes leads to modify the prescription of Calabi-Yau or orbifold
compactifications and new non-perturbative are possible. In these sections we
will discuss some of these interesting topics.
truecm
Subsections



Next: Toroidal Compactification, -duality and
Up: STRINGS, BRANES AND DUALITY1
Previous: Calabi-Yau Compactifications in Perturbative
root
2001-01-15