


Next: M-Theory
Up: Non-perturbative String Theory
Previous: Non-perturbative String Theory
We have described the massless spectrum of the five consistent superstring
theories in ten dimensions. Additional theories can be constructed in lower dimensions
by compactification of some of the ten dimensions. Thus the ten-dimensional spacetime
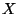 looks like the product
looks like the product
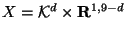 , with
, with  a
suitable compact
manifold or orbifold. Depending on which compact space is taken, it will be the
quantity of preserved supersymmetry.
All five theories and their compactifications are parametrized by: the string coupling
constant
a
suitable compact
manifold or orbifold. Depending on which compact space is taken, it will be the
quantity of preserved supersymmetry.
All five theories and their compactifications are parametrized by: the string coupling
constant 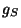 , the geometry of the compact manifold
, the geometry of the compact manifold  , the topology of
, the topology of  and the
spectrum of bosonic fields in the NS-NS and the R-R sectors. Thus one can
define the string moduli space
and the
spectrum of bosonic fields in the NS-NS and the R-R sectors. Thus one can
define the string moduli space  of each one of the theories as the space
of all associated parameters. Moreover, it can be defined a map between two of these
moduli spaces. The dual map is defined as the map
of each one of the theories as the space
of all associated parameters. Moreover, it can be defined a map between two of these
moduli spaces. The dual map is defined as the map
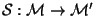 between the moduli spaces
between the moduli spaces  and
and 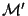 such that the strong/weak
region of
such that the strong/weak
region of  is interchanged with the weak/strong region of
is interchanged with the weak/strong region of 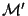 .
One can define another map
.
One can define another map
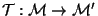 which
interchanges the volume
which
interchanges the volume 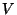 of
of  for
for 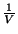 . One example of the map
. One example of the map 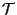 is the equivalence, by T-duality, between the theories Type IIA compactified on
is the equivalence, by T-duality, between the theories Type IIA compactified on 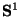 at radius
at radius  and the Type IIB theory on
and the Type IIB theory on 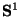 at raduis
at raduis 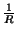 . The
theories HE and HO constitutes another example of the
. The
theories HE and HO constitutes another example of the
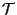 map. In this section we will follows the Sen's review [20]. Another
useful references are [21,22,23,24,25]. Type IIB theory is self-dual with
respect the
map. In this section we will follows the Sen's review [20]. Another
useful references are [21,22,23,24,25]. Type IIB theory is self-dual with
respect the 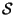 map.
truecm
Type IIB-IIB Duality
The Type IIB theory is self-dual. In order to see that write the bosonic part of the
action of Type IIB supersting theory
map.
truecm
Type IIB-IIB Duality
The Type IIB theory is self-dual. In order to see that write the bosonic part of the
action of Type IIB supersting theory
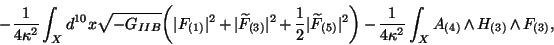 |
(49) |
where
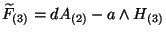 and
and
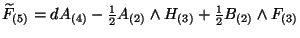 .
This action is clearly invariant under
.
This action is clearly invariant under
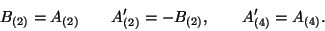 |
(50) |
This symmetry leads to an identification
of a fundamental string F1 with a D1-brane (
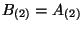 ) and the interchanging of
a pair of D3-branes.
truecm
Type I-SO(32)-Heterotic Duality
In order to analyze the duality between Type I and SO(32) heterotic string theories we
recall the spectrum of both theories. These fields are the dynamical fields
of a supergravity Lagrangian in ten dimensions. Type I string theory has in the
NS-NS sector the following fields: the metric
) and the interchanging of
a pair of D3-branes.
truecm
Type I-SO(32)-Heterotic Duality
In order to analyze the duality between Type I and SO(32) heterotic string theories we
recall the spectrum of both theories. These fields are the dynamical fields
of a supergravity Lagrangian in ten dimensions. Type I string theory has in the
NS-NS sector the following fields: the metric
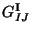 , the dilaton
, the dilaton 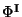 and
in the R-R sector: the antisymmetric tensor
and
in the R-R sector: the antisymmetric tensor
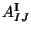 . Also there are 496
gauge bosons
. Also there are 496
gauge bosons
 in the adjoint representation of the gauge group SO(32). For
the SO(32) heterotic string theory the spectrum consist of: the spacetime metric
in the adjoint representation of the gauge group SO(32). For
the SO(32) heterotic string theory the spectrum consist of: the spacetime metric
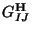 , the dilaton field
, the dilaton field 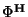 , the antisymmetric tensor
, the antisymmetric tensor
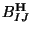 and 496 gauge fields
and 496 gauge fields
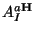 in the adjoint representation of SO(32). Both
theories have
in the adjoint representation of SO(32). Both
theories have 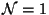 spacetime supersymmetry. The effective action for the
massless fields of the Type I supergravity effective action
spacetime supersymmetry. The effective action for the
massless fields of the Type I supergravity effective action 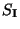 is defined as
is defined as
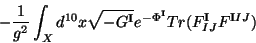 |
(51) |
where
![$\widetilde{F}_{(3)} = F_{(3)} - {\alpha ' \over 4} [\omega_{3Y}(A) - \omega_{3L}
(\omega)].$](img457.gif) While the heterotic action
While the heterotic action 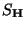 is defined as
is defined as
![\begin{displaymath}
S_{\bf H} = {1 \over 2 \kappa^2} \int_X d^{10}x \sqrt{-G^{\...
... {\alpha ' \over 8} Tr ( F^{\bf H}_{IJ} F^{{\bf H}IJ}) \bigg]
\end{displaymath}](img459.gif) |
(52) |
where
![$\widetilde{H}_{(3)} = dB_{(2)} - {\alpha ' \over 4} [\omega_{3Y}(A) - \omega_{3L}
(\omega)].$](img460.gif) The comparison of these two actions leads to the following identification of the fields
The comparison of these two actions leads to the following identification of the fields
 |
(53) |
This give us many information, the first relation tell us that the metrics of both
theories are the same. The second relation interchanges the 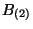 field in the
NS-NS sector and the
field in the
NS-NS sector and the 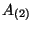 field in the R-R sector. That implies the interchanging of
heterotic strings
and Type I D1-branes. The third relation identifies the gauge fields coming from the
Chan-Paton factors from the Type I side with the gauge fields coming from the 16
compactified internal dimensions of the heterotic string. Finally, the opposite sign for
the dilaton relation means that the string coupling constant
field in the R-R sector. That implies the interchanging of
heterotic strings
and Type I D1-branes. The third relation identifies the gauge fields coming from the
Chan-Paton factors from the Type I side with the gauge fields coming from the 16
compactified internal dimensions of the heterotic string. Finally, the opposite sign for
the dilaton relation means that the string coupling constant 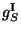 is inverted
is inverted
 within this identification, and interchanges the strong and weak
couplings of both theories leading to the explicit realization of the
within this identification, and interchanges the strong and weak
couplings of both theories leading to the explicit realization of the 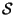 map.
truecm
map.
truecm



Next: M-Theory
Up: Non-perturbative String Theory
Previous: Non-perturbative String Theory
root
2001-01-15