


Next: Horava-Witten Theory
Up: Non-perturbative String Theory
Previous: Strong-Weak Coupling String Duality
We have described how to construct dual pairs of string theories. By the uses of the
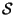 and the
and the 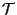 maps a network of theories can be constructed in various
dimensions all of them related by dualities. However new theories can emerge from this
picture, this is the case of M-theory. M-theory (the name come from `mystery', `magic',
`matrix', `membrane', etc.) was originally defined as the strong coupling limit for Type
IIA string theory [21].
It is known that Type IIA theory can be
obtained from the dimensional reduction of the eleven dimensional supergravity theory (a
theory known from the 70's years) and given by the Cremmer-Julia-Scherk Lagrangian
maps a network of theories can be constructed in various
dimensions all of them related by dualities. However new theories can emerge from this
picture, this is the case of M-theory. M-theory (the name come from `mystery', `magic',
`matrix', `membrane', etc.) was originally defined as the strong coupling limit for Type
IIA string theory [21].
It is known that Type IIA theory can be
obtained from the dimensional reduction of the eleven dimensional supergravity theory (a
theory known from the 70's years) and given by the Cremmer-Julia-Scherk Lagrangian
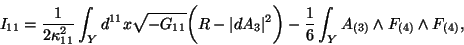 |
(54) |
where 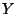 is the eleven dimensional manifold. If we assume that the eleven-dimensional
spacetime factorizes as
is the eleven dimensional manifold. If we assume that the eleven-dimensional
spacetime factorizes as
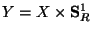 , where the compact dimension has
radius
, where the compact dimension has
radius  . Usual Kaluza-Klein dimensional reduction leads to get the ten-dimensional metric,
an scalar field and a vector field.
. Usual Kaluza-Klein dimensional reduction leads to get the ten-dimensional metric,
an scalar field and a vector field.  from the eleven dimensional theory leads to
from the eleven dimensional theory leads to
 and
and 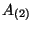 in the ten-dimensional theory. The scalar field turn out too be proportional
to the dilaton field of the NS-NS sector of the Type IIA theory. The vector field from the KK
compactification can be identified with the
in the ten-dimensional theory. The scalar field turn out too be proportional
to the dilaton field of the NS-NS sector of the Type IIA theory. The vector field from the KK
compactification can be identified with the 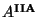 field of the R-R sector. From the
three-form in eleven dimensions are obtained the RR field
field of the R-R sector. From the
three-form in eleven dimensions are obtained the RR field  of the Type IIA theory. Fin ally,
the
of the Type IIA theory. Fin ally,
the 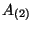 field is identified with the NS-NS B-field of field strength
field is identified with the NS-NS B-field of field strength
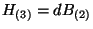 .
Thus the eleven-dimensional Lagrangian leads to the Type IIA supergravity in the weak coupling
limit (
.
Thus the eleven-dimensional Lagrangian leads to the Type IIA supergravity in the weak coupling
limit (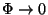 or
or  ). The ten-dimensional IIA supergravity describing the bosonic
part of the low energy
limit of the Type IIA superstring theory is
). The ten-dimensional IIA supergravity describing the bosonic
part of the low energy
limit of the Type IIA superstring theory is
 |
(55) |
where
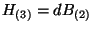 ,
,
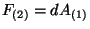 and
and
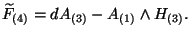 It is conjectured that there exist an eleven dimensional
fundamental theory whose low energy limit is the 11 dimensional supergravity theory
and that it is the strong coupling limit of the Type IIA superstring theory.
At the present time the degrees of freedom (dof's) are still unknown, through at the
macroscopic level they should be membranes and fivebranes (also called M2-branes and
M5-branes).
truecm
It is conjectured that there exist an eleven dimensional
fundamental theory whose low energy limit is the 11 dimensional supergravity theory
and that it is the strong coupling limit of the Type IIA superstring theory.
At the present time the degrees of freedom (dof's) are still unknown, through at the
macroscopic level they should be membranes and fivebranes (also called M2-branes and
M5-branes).
truecm



Next: Horava-Witten Theory
Up: Non-perturbative String Theory
Previous: Strong-Weak Coupling String Duality
root
2001-01-15