


Next: References
Up: STRINGS, BRANES AND DUALITY1
Previous: F-Theory
M-theory Vacua
In this section we review some Calabi-Yau compactifications of M and F-Theories. In the first
part of these lecture we described the perturbative CY compactifications, the purpose of the present
section
is see how these compactifications behaves in the light of duality and D-brane theory (for
excellent reviews see [26,27]). The presence of D-branes or M-branes, in the
case of M theory, modifies the perturbative CY compactifications, here we briefly
describe these modifications.
Assume that the eleven-dimensional spacetime is
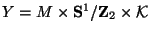 , with
, with  being a Calabi-Yau three-fold. Here we consider that
being a Calabi-Yau three-fold. Here we consider that
 is a elliptic fibration, since they are favored by CY compactifications of
M and F theories. These spacetime corresponds of having two copies (planes) of
is a elliptic fibration, since they are favored by CY compactifications of
M and F theories. These spacetime corresponds of having two copies (planes) of
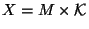 at the two boundaries of the orbifold. According to the Horava-Witten theory, anomalies
cancellation involves that one
at the two boundaries of the orbifold. According to the Horava-Witten theory, anomalies
cancellation involves that one 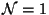 vector supermultiplet of the
vector supermultiplet of the 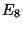 super
Yang-Mills theory has to be captured in each orbifold fixed plane
super
Yang-Mills theory has to be captured in each orbifold fixed plane 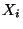 ,
, 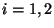 .
According to the perturbative description it is necessary to specify now two stable or semi-stable
holomorphic vector
bundles
.
According to the perturbative description it is necessary to specify now two stable or semi-stable
holomorphic vector
bundles 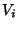 on
on  with arbitrary group structure. For the heterotic-M theory
compactifications the structure group has to be a subgroup of
with arbitrary group structure. For the heterotic-M theory
compactifications the structure group has to be a subgroup of 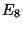 .
For simplicity we restrict ourselves to SU
.
For simplicity we restrict ourselves to SU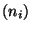 vector bundles
vector bundles 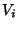 over
over  . The presence
of fivebranes is of extreme importance here, since it allows more flexibility to construct such
vector bundles
. The presence
of fivebranes is of extreme importance here, since it allows more flexibility to construct such
vector bundles 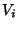 which leads to more realistic particle physics models. From the modified
Bianchi identity and the anomaly cancellation condition of the orbifold system and the
fivebranes wrapped on holomorphic two-cycles of
which leads to more realistic particle physics models. From the modified
Bianchi identity and the anomaly cancellation condition of the orbifold system and the
fivebranes wrapped on holomorphic two-cycles of  , leads that these bundles are subject to
the cohomological constraint of the second Chern
classes
, leads that these bundles are subject to
the cohomological constraint of the second Chern
classes
![$c_2(V_1) + c_2(V_2) + [W] = c_2(T{\cal K})$](img501.gif) , where
, where ![$[W]$](img502.gif) is the topological class
associated to the fivebranes.
The description of the low-energy physics requires of the computation of the first three
Chern classes of the holomorphic bundles
is the topological class
associated to the fivebranes.
The description of the low-energy physics requires of the computation of the first three
Chern classes of the holomorphic bundles 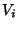 over
over  and thus determine completely
a non-perturbative vacuum. M and F theories compactifications
require that
and thus determine completely
a non-perturbative vacuum. M and F theories compactifications
require that  must be a holomorphic elliptic fibration. Thus the construction of these
bundles are nontrivial.
truecm
Construction of the Gauge Bundles over Elliptic Fibrations
An holomorphic elliptically fibered Calabi-Yau three-fold is a fibration
must be a holomorphic elliptic fibration. Thus the construction of these
bundles are nontrivial.
truecm
Construction of the Gauge Bundles over Elliptic Fibrations
An holomorphic elliptically fibered Calabi-Yau three-fold is a fibration
where 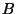 is an auxiliary complex two-dimensional manifold,
is an auxiliary complex two-dimensional manifold, 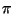 is an holomorphic mapping,
and for each
is an holomorphic mapping,
and for each  ,
,
 is isomorphic to an elliptic curve
is isomorphic to an elliptic curve 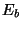 . In
addition we require the existence of a global section
. In
addition we require the existence of a global section
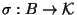 of this
fibration.
The elliptic fibration can be characterized by a single line bundle
of this
fibration.
The elliptic fibration can be characterized by a single line bundle 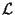 over
over 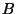 ,
,
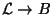 , whose fiber is the cotangent space to the elliptic curve,
, whose fiber is the cotangent space to the elliptic curve, 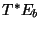 . This
bundle satisfies the condition:
. This
bundle satisfies the condition:
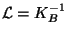 with
with 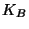 being the
canonical bundle of
being the
canonical bundle of 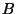 , under the usual condition that the canonical bundle
, under the usual condition that the canonical bundle
 has vanishing first Chern class
has vanishing first Chern class
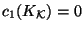 . While the global section is
specified giving the bundles
. While the global section is
specified giving the bundles
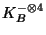 and
and
 .
These conditions are known to be satisfied by
base spaces
.
These conditions are known to be satisfied by
base spaces 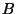 corresponding to del Pezzo, Hirzebruch and Enriques surfaces.
For elliptic fibrations, Friedman, Morgan and Witten [28] found that the second Chern class of
the holomorphic tangent bundle
corresponding to del Pezzo, Hirzebruch and Enriques surfaces.
For elliptic fibrations, Friedman, Morgan and Witten [28] found that the second Chern class of
the holomorphic tangent bundle 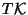 can be written in terms of the Chern classes of
can be written in terms of the Chern classes of 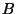 as
follows
as
follows
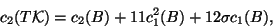 |
(59) |
where 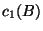 and
and 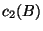 are the first and the second class of
are the first and the second class of 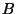 and
and 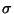 is a two-form
and represents the
Poincaré dual of mentioned global section of the elliptic fibration.
One can construct the semi-stable SU
is a two-form
and represents the
Poincaré dual of mentioned global section of the elliptic fibration.
One can construct the semi-stable SU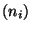 holomorphic bundles
holomorphic bundles 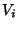 on
on  through
the specification of two line bundles
through
the specification of two line bundles
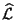 with first Chern class
with first Chern class
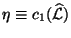 and
and
 with corresponding first
Chern class
with corresponding first
Chern class
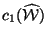 depending on some parameters
depending on some parameters
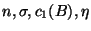 and
and
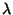 . Thus the bundle
. Thus the bundle
 is completely specified by the elliptic fibration and
the line bundle
is completely specified by the elliptic fibration and
the line bundle
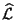 . The condition that
. The condition that
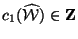 leads to the relation
leads to the relation
 for
for 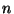 odd and
odd and 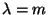 and
and 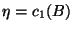 mod 2, for
mod 2, for 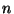 even,
even, 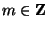 . Thus the Chern classes of the
SU
. Thus the Chern classes of the
SU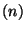 gauge bundle
gauge bundle 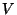 are
In order to construct realistic particle physics models we take a given base space
are
In order to construct realistic particle physics models we take a given base space 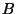 and compute its corresponding Chern classes
and compute its corresponding Chern classes 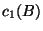 and
and 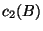 . Compute the
relevant Chern classes of the SU
. Compute the
relevant Chern classes of the SU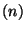 gauge bundles
gauge bundles 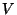 . The constraints above reduce the
number of consistent physical non-perturbative vacua. Given appropriate
. The constraints above reduce the
number of consistent physical non-perturbative vacua. Given appropriate 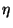 and
and
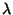 one can determine completely the physical Chern classes.
truecm
Counting the Number of Families
The number of families of leptons and quarks of the four-dimensional theory is related to the number
of zero modes of the Dirac operator
coupled to gauge field, which is a connection
on the SU
one can determine completely the physical Chern classes.
truecm
Counting the Number of Families
The number of families of leptons and quarks of the four-dimensional theory is related to the number
of zero modes of the Dirac operator
coupled to gauge field, which is a connection
on the SU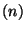 bundle
bundle 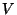 on the
elliptic fibered Calabi-Yau three-fold
on the
elliptic fibered Calabi-Yau three-fold  . In order to count the number of the
chiral fermionic zero modes, one can consider the following cases:
The matter representations appear in the fundamental representation of the gauge group
SU
. In order to count the number of the
chiral fermionic zero modes, one can consider the following cases:
The matter representations appear in the fundamental representation of the gauge group
SU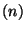 . The index of the Dirac operator gives
. The index of the Dirac operator gives
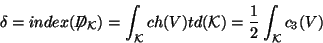 |
(60) |
where 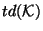 is the Todd class of
is the Todd class of  . From explitit formula
for
. From explitit formula
for 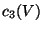 we get that the number of generations is given by
we get that the number of generations is given by
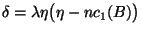 .
truecm
.
truecm
Acknowledgements
I am very grateful to F. Quevedo, E. Cifuentes and W. Aldana for the opportunity to give these
lectures at the Universidad de San Carlos, Guatemala.
It is a pleasure to thank them and the Universidad de San Carlos for their hospitality.



Next: References
Up: STRINGS, BRANES AND DUALITY1
Previous: F-Theory
root
2001-01-15