


Next: Non-perturbative Calabi-Yau Compactifications
Up: Non-perturbative String Theory
Previous: Horava-Witten Theory
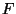 -Theory was formulated by C. Vafa, looking for an analog theory to M-Theory for
describing non-perturbative compactifications of Type IIB theory (for a review see
[24,20]). Usually in perturbative compactifications the parameter
-Theory was formulated by C. Vafa, looking for an analog theory to M-Theory for
describing non-perturbative compactifications of Type IIB theory (for a review see
[24,20]). Usually in perturbative compactifications the parameter
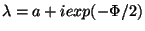 is taken to be constant.
is taken to be constant. 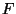 -theory generalizes this fact by
considering variable
-theory generalizes this fact by
considering variable 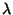 . Thus
. Thus 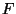 -theory is defined as a twelve-dimensional
theory whose compactification on the elliptic fibration
-theory is defined as a twelve-dimensional
theory whose compactification on the elliptic fibration
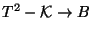 , gives
the Type IIB theory compactified on
, gives
the Type IIB theory compactified on 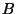 (for a suitable space
(for a suitable space 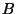 ) with the
identification of
) with the
identification of
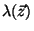 with the modulus
with the modulus 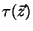 of the torus
of the torus
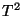 . These compactifications can be related to the
. These compactifications can be related to the  -theory compactifications
through the known
-theory compactifications
through the known 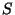 mapping
mapping
 and the
and the 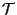 map
between Type IIA and IIB theories. This gives
map
between Type IIA and IIB theories. This gives
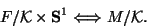 |
(57) |
Thus the spectrum of massless states of 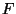 -theory compactifications can be
described in terms of
-theory compactifications can be
described in terms of  -theory. Other interesting
-theory. Other interesting 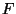 -theory compactifications
are the Calabi-Yau compactifications
-theory compactifications
are the Calabi-Yau compactifications
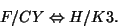 |
(58) |
truecm
root
2001-01-15