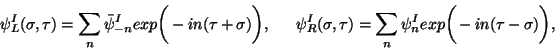Next: Type I Superstrings
Up: Perturbative String and Superstring
Previous: Interacting Strings and the
In bosonic string theory there are two bold problems. The first one is the presence
of tachyons in the spectrum. The second one is that there are no spacetime fermions.
Here is where superstrings come to the rescue. A superstring is described, despite of
the usual bosonic fields 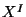 , by
fermionic fields
, by
fermionic fields
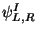 on the worldsheet
on the worldsheet  . Which satisfy anticommutation rules and
where
the
. Which satisfy anticommutation rules and
where
the 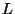 and
and  denote the left and right worldsheet chirality respectively. The action for the
superstring is given by
denote the left and right worldsheet chirality respectively. The action for the
superstring is given by
 |
(25) |
where  and
and 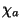 are the superpartners of
are the superpartners of 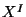 and the tetrad field
and the tetrad field 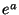 respectively.
In the superconformal gauge (
respectively.
In the superconformal gauge (
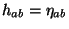 and
and 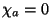 ) and in light-cone
coordinates it can be reduced to
) and in light-cone
coordinates it can be reduced to
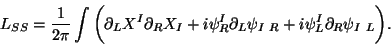 |
(26) |
In analogy to the bosonic case, the local dynamics
of the worldsheet metric is manifestly conformal anomaly free at the quantum level if
the critical
spacetime dimension 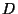 is 10. Thus the string
oscillates in the 8 transverse dimensions. The action (25) is
invariant under:
is 10. Thus the string
oscillates in the 8 transverse dimensions. The action (25) is
invariant under:  worldsheet supersymmetry,
worldsheet supersymmetry,  Weyl transformations,
Weyl transformations,
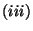 super-Weyl transformations,
super-Weyl transformations, 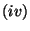 Poincaré transformations and
Poincaré transformations and
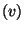 Worldsheet reparametrizations. The equation of motion for the
Worldsheet reparametrizations. The equation of motion for the 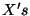 fields is
the same that in the bosonic case (Laplace equation) and
whose general solution is given by Eqs. (5) or (6). Equation of
motion for the fermionic field is the Dirac equation in two dimensions.
Constraints here are more involved and they are called the super-Virasoro
constraints. However in the light-cone gauge, everything simplifies and
the transverse coordinates (eight coordinates) become the bosonic physical degrees
of freedom together with their corresponding supersymmetric partners. Analogously
to the bosonic case,
massless states of the spectrum come into representations of the little group SO(8)
which is a subgroup of SO
fields is
the same that in the bosonic case (Laplace equation) and
whose general solution is given by Eqs. (5) or (6). Equation of
motion for the fermionic field is the Dirac equation in two dimensions.
Constraints here are more involved and they are called the super-Virasoro
constraints. However in the light-cone gauge, everything simplifies and
the transverse coordinates (eight coordinates) become the bosonic physical degrees
of freedom together with their corresponding supersymmetric partners. Analogously
to the bosonic case,
massless states of the spectrum come into representations of the little group SO(8)
which is a subgroup of SO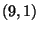 , while that the massive states lie into representations of the little
group SO
, while that the massive states lie into representations of the little
group SO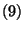 .
For the closed string there are two possibilities for the boundary conditions of fermions:
.
For the closed string there are two possibilities for the boundary conditions of fermions:
 periodic
boundary conditions (Ramond (R) sector)
periodic
boundary conditions (Ramond (R) sector)
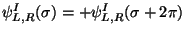 and
and  anti-periodic boundary conditions
(Neveu-Schwarz (NS) sector)
anti-periodic boundary conditions
(Neveu-Schwarz (NS) sector)
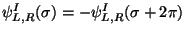 .
Solutions of Dirac equation satisfying these boundary conditions are
.
Solutions of Dirac equation satisfying these boundary conditions are
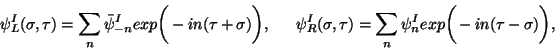 |
(27) |
where
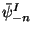 and
and 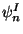 are fermionic modes of left and right movers
respectively.
In the case
of the fermions in the R sector
are fermionic modes of left and right movers
respectively.
In the case
of the fermions in the R sector
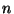 is integer and it is semi-integer in the NS sector.
The quantization of the
superstring come from the promotion of the fields
is integer and it is semi-integer in the NS sector.
The quantization of the
superstring come from the promotion of the fields 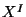 and
and  to operators
whose oscillator variables are operators satisfying the relations
to operators
whose oscillator variables are operators satisfying the relations
![$[\alpha^I _n, \alpha^J _m]_-~= n\delta_{m+n,0}\eta^{IJ}$](img175.gif) and
and
![$[\psi^I _n,\psi^J _m]_+~=~\eta^{IJ}\delta_{m+n,0},$](img176.gif) where
where ![$[,]_-$](img177.gif) and
and
![$[,]_+$](img178.gif) stand for commutator and anti-commutator respectively.
The zero modes of
stand for commutator and anti-commutator respectively.
The zero modes of 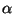 are diagonal in the Fock space and its
eigenvalue can be identified with its momentum. For the NS sector there is no
fermionic zero modes but they can exist for the R sector and they satisfy a Clifford
algebra
are diagonal in the Fock space and its
eigenvalue can be identified with its momentum. For the NS sector there is no
fermionic zero modes but they can exist for the R sector and they satisfy a Clifford
algebra
![$[\psi^I _0,\psi^J _0]_+~=~\eta^{IJ}$](img180.gif) . The Hamiltonian for the
closed superstring is given by
. The Hamiltonian for the
closed superstring is given by
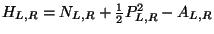 . For the
NS sector
. For the
NS sector 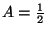 , while for the R sector
, while for the R sector  . The mass is given by
. The mass is given by
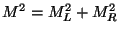 with
with
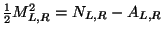 .
There are five consistent superstring theories: Type IIA, IIB, Type I, SO(32) and
.
There are five consistent superstring theories: Type IIA, IIB, Type I, SO(32) and
 heterotic strings, represented by HO and HE respectively. In what follows of this
section we briefly describe the spectrum
in
each one of them.
truecm
Type II Superstring Theories
In this case the theory consist of closed strings only. They are theories with
heterotic strings, represented by HO and HE respectively. In what follows of this
section we briefly describe the spectrum
in
each one of them.
truecm
Type II Superstring Theories
In this case the theory consist of closed strings only. They are theories with 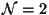 spacetime supersymmetry. There are 8 scalar fields (representing
the 8 transverse coordinates to the string) and one Weyl-Majorana spinor. There are
8 left-moving and 8 right-moving fermions.
In the NS sector there is still a tachyon in the ground state. But in the
supersymmetric case this problem can be solved through the introduction of
the called GSO projection. This projection eliminates the tachyon in the NS sector
and it acts in the R sector as a ten-dimensional spacetime chirality operator. That means
that the
application of the GSO projection operator defines the chirality of a
massless spinor in the R sector. Thus from the left and right
moving sectors, one can construct states in
four different sectors:
spacetime supersymmetry. There are 8 scalar fields (representing
the 8 transverse coordinates to the string) and one Weyl-Majorana spinor. There are
8 left-moving and 8 right-moving fermions.
In the NS sector there is still a tachyon in the ground state. But in the
supersymmetric case this problem can be solved through the introduction of
the called GSO projection. This projection eliminates the tachyon in the NS sector
and it acts in the R sector as a ten-dimensional spacetime chirality operator. That means
that the
application of the GSO projection operator defines the chirality of a
massless spinor in the R sector. Thus from the left and right
moving sectors, one can construct states in
four different sectors:  NS-NS,
NS-NS,
 NS-R,
NS-R,  R-NS and
R-NS and  R-R. Taking into account the two types of
chirality
R-R. Taking into account the two types of
chirality 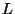 and
and  one has two possibilities:
one has two possibilities:
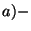 The GSO projections on the left and right fermions produce different
chirality in the ground state of the R sector (Type IIA).
The GSO projections on the left and right fermions produce different
chirality in the ground state of the R sector (Type IIA).
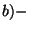 GSO projection are equal in left and right sectors and the ground states
in the R sector, have the same chirality (Type IIB). Thus the spectrum for the Type IIA
and
IIB superstring theories is:
GSO projection are equal in left and right sectors and the ground states
in the R sector, have the same chirality (Type IIB). Thus the spectrum for the Type IIA
and
IIB superstring theories is:
- Type IIA
The NS-NS sector has a symmetric tensor field
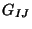 (spacetime metric), an
antisymmetric
tensor field
(spacetime metric), an
antisymmetric
tensor field
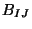 and a scalar field
and a scalar field 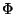 (dilaton). In the R-R sector there is a vector field
(dilaton). In the R-R sector there is a vector field
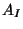 associated with a 1-form
associated with a 1-form 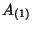 (
(
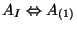 ) and a rank 3
totally
antisymmetric tensor
) and a rank 3
totally
antisymmetric tensor
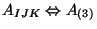 and by Hodge duality in ten
dimensions also we have
and by Hodge duality in ten
dimensions also we have 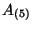 ,
,  and
and 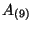 . In general the R-R sector
consist of
. In general the R-R sector
consist of 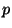 -forms
-forms
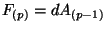 (where
(where 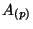 are called RR fields) on the
ten-dimensional spacetime
are called RR fields) on the
ten-dimensional spacetime 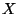 with
with 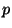 even i.e.
even i.e.
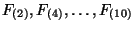 . In the NS-R and R-NS sectors we have
two gravitinos with opposite
chirality and the supersymmetric partners of the mentioned bosonic fields.
. In the NS-R and R-NS sectors we have
two gravitinos with opposite
chirality and the supersymmetric partners of the mentioned bosonic fields.
- Type IIB
In the NS-NS sector Type IIB theory has exactly the same spectrum that of Type IIA theory.
On the R-R sector it has a scalar field
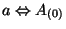 (the axion field), an
antisymmetric tensor
field
(the axion field), an
antisymmetric tensor
field
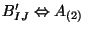 and a rank 4 totally antisymmetric tensor
and a rank 4 totally antisymmetric tensor
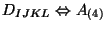 whose field strength is self-dual i.e.,
whose field strength is self-dual i.e.,
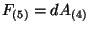 with
with
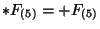 . Similar than for the case of Type IIA
theory one has also the Hodge dual fields
. Similar than for the case of Type IIA
theory one has also the Hodge dual fields 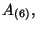
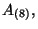
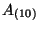 .
In general,
RR fields in Type IIB theory are given by
.
In general,
RR fields in Type IIB theory are given by 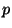 -forms
-forms
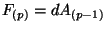 on the spacetime
on the spacetime
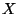 with
with 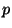 odd
i.e.
odd
i.e.
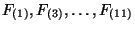 . The NS-R and R-NS sectors do contain two
gravitinos
with the
same chirality and the corresponding fermionic matter.
. The NS-R and R-NS sectors do contain two
gravitinos
with the
same chirality and the corresponding fermionic matter.
truecm



Next: Type I Superstrings
Up: Perturbative String and Superstring
Previous: Interacting Strings and the
root
2001-01-15