



Next: DE LA RELATIVIDAD ESPECIAL
Up: INTRODUCCIÓN A LA TEORÍA
Previous: Marcos inerciales locales
Índice General
En el espacio tridimensional, se puede expresar las coordenadas cartesianas 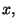
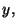
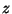 como función de otras coordenadas generales
como función de otras coordenadas generales 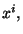 de
modo que las primera son función de éstas últimas. De esta
manera, en forma general, se obtiene que el tensor métrico es
de
modo que las primera son función de éstas últimas. De esta
manera, en forma general, se obtiene que el tensor métrico es
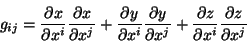 |
(1.9) |
En un espacio plano o euclideano
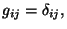 donde
donde
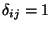 si
si 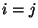 y
y
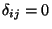 si
si 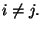 En este caso la
métrica es
En este caso la
métrica es
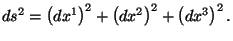 Este concepto se puede extender al espacio-tiempo de cuatro
dimensiones sin ningún problema, utilizando coordenadas
Este concepto se puede extender al espacio-tiempo de cuatro
dimensiones sin ningún problema, utilizando coordenadas 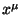 para describir los eventos. En cuatro dimensiones el tensor métrico
tendrá 16 componentes, de las cuales 10 son independientes en virtud de
que este tensor es simétrico, es decir,
para describir los eventos. En cuatro dimensiones el tensor métrico
tendrá 16 componentes, de las cuales 10 son independientes en virtud de
que este tensor es simétrico, es decir,
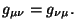 Es importante notar que en el espacio euclideano tridimensional,
Es importante notar que en el espacio euclideano tridimensional, 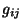 simpre puede ser reducido a
simpre puede ser reducido a 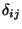 en todo el espacio. En el
espacio-tiempo generalmente es posible hacer lo mismo, aunque sólo
localmente; es decir, reducir
en todo el espacio. En el
espacio-tiempo generalmente es posible hacer lo mismo, aunque sólo
localmente; es decir, reducir 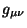 a
a
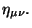 Por lo
tanto, en presencia de un campo gravitacional no es posible cubrir todo el
espacio con un único marco inercial.
Además en el espacio euclideano la distancia que separa a dos puntos
siempre es mayor que cero. Esto no sucede en el espacio-tiempo, en donde la
distancia entre dos eventos puede ser positiva, negativa o cero. Una
separación positiva expresa la posibilidad de que los dos eventos
estén conectados causalmente y se puede encontrar un marco de referencia
en el cual los eventos ocurran en el mismo lugar. Si la separación es
negativa, los eventos no están conectados causalmente y uno no puede
influir en el otro. Se puede encontrar un marco de referencia en donde estos
eventos sean simultáneos. El caso en que la separación entre eventos
sea cero se satisface sólo para una señal electromagnética o un
pulso de luz, que viaje entre los dos eventos. [4]
Por lo
tanto, en presencia de un campo gravitacional no es posible cubrir todo el
espacio con un único marco inercial.
Además en el espacio euclideano la distancia que separa a dos puntos
siempre es mayor que cero. Esto no sucede en el espacio-tiempo, en donde la
distancia entre dos eventos puede ser positiva, negativa o cero. Una
separación positiva expresa la posibilidad de que los dos eventos
estén conectados causalmente y se puede encontrar un marco de referencia
en el cual los eventos ocurran en el mismo lugar. Si la separación es
negativa, los eventos no están conectados causalmente y uno no puede
influir en el otro. Se puede encontrar un marco de referencia en donde estos
eventos sean simultáneos. El caso en que la separación entre eventos
sea cero se satisface sólo para una señal electromagnética o un
pulso de luz, que viaje entre los dos eventos. [4]




Next: DE LA RELATIVIDAD ESPECIAL
Up: INTRODUCCIÓN A LA TEORÍA
Previous: Marcos inerciales locales
Índice General
enrique pazos
2000-09-27