



Next: INTRODUCCIÓN A LA TEORÍA
Up: Índice de Figuras
Previous: GLOSARIO
Índice General
El presente trabajo es una investigación realizada en la rama de la
teoría general de la relatividad. Dicho trabajo fue realizado en el
Instituto de Física de la Universidad de Guanajuato, México, con
la asesoría del Dr. José Socorro García Díaz.
El propósito de esta investigación es presentar una manera
sistemática de calcular una función lagrangiana para el campo
gravitacional tomando en cuenta la fuente del mismo, es decir, en presencia
de materia. Partiendo de este lagrangiano se pueden calcular las ecuaciones
clásicas de campo, las cuales contienen la información acerca del
comportamiento del campo gravitacional. Debido a la no linealidad de las
ecuaciones de Einstein, en algunos casos este comportamiento sólo puede
ser hallado de manera aproximada. Haciendo una analogía con los
sistemas mecánicos, es posible aplicar las ideas de cuantización
canónica al hamiltoniano del sistema, calculado a partir del
lagrangiano. De esta manera la gravedad puede ser cuantizada en ciertos
modelos matemáticos.
El trabajo se compone esencialmente de cuatro capítulos. En el primero
de ellos se hace una presentación de las ideas que condujeron a la
creación de la teoría especial de la relatividad. Asimismo, se
presentan los conceptos más importantes de dicha teoría.
En el segundo capítulo se expone la incompatibilidad de la teoría de
la relatividad especial y la relatividad general, haciendo ver que la
descripción de la gravedad no puede lograrse en un espacio-tiempo plano.
En el resto del capítulo se tratan los conceptos matemáticos que
hacen posible describir la curvatura del espacio-tiempo. Se finaliza con la
relación que existe entre la materia y la curvatura del espacio, dada
por la ecuación de campo de Einstein,
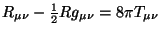 .
El tercer capítulo comienza
con una introducción
al formalismo ADM. Posteriormente, se
presenta el procedimiento matemático mediante el cual se originan las
variables ADM, la construcción del lagrangiano en función de estas
variables y la obtención del hamiltoniano a partir del lagrangiano. Se
concluye con la manera de obtener la parte del lagrangiano que resulta de
considerar una distribución de materia y energía en el espacio.
En el cuarto capítulo se aplican los conceptos generales desarrollados
anteriormente para calcular el lagrangiano a partir de una métrica dada,
considerando la existencia de un fluido perfecto de materia. Se calculan las
ecuaciones de movimiento a partir del lagrangiano. Independientemente, estas
ecuaciones también son calculadas mediante la ecuación de campo de
Einstein. Se llega al resultado de que ambos métodos dan las mismas
ecuaciones. Por último, se presenta la solución de dichas ecuaciones
de la forma más general que se pudo hallar y para un caso simplicado del
modelo original.
La solución a las ecuaciones no es completa. Esto es debido a la
complejidad de las mismas, pues se trata de un sistema de ecuaciones
diferenciales parciales, no lineales y no homogéneas. Estos sistemas de
ecuaciones difícilmente aceptan una solución general. Por lo que se
hizo una simplificación al modelo original con lo cual se encontró una
solución a las ecuaciones.
Finalmente, se incluye un apéndice acerca del cálculo del escalar de
curvatura
.
El tercer capítulo comienza
con una introducción
al formalismo ADM. Posteriormente, se
presenta el procedimiento matemático mediante el cual se originan las
variables ADM, la construcción del lagrangiano en función de estas
variables y la obtención del hamiltoniano a partir del lagrangiano. Se
concluye con la manera de obtener la parte del lagrangiano que resulta de
considerar una distribución de materia y energía en el espacio.
En el cuarto capítulo se aplican los conceptos generales desarrollados
anteriormente para calcular el lagrangiano a partir de una métrica dada,
considerando la existencia de un fluido perfecto de materia. Se calculan las
ecuaciones de movimiento a partir del lagrangiano. Independientemente, estas
ecuaciones también son calculadas mediante la ecuación de campo de
Einstein. Se llega al resultado de que ambos métodos dan las mismas
ecuaciones. Por último, se presenta la solución de dichas ecuaciones
de la forma más general que se pudo hallar y para un caso simplicado del
modelo original.
La solución a las ecuaciones no es completa. Esto es debido a la
complejidad de las mismas, pues se trata de un sistema de ecuaciones
diferenciales parciales, no lineales y no homogéneas. Estos sistemas de
ecuaciones difícilmente aceptan una solución general. Por lo que se
hizo una simplificación al modelo original con lo cual se encontró una
solución a las ecuaciones.
Finalmente, se incluye un apéndice acerca del cálculo del escalar de
curvatura 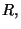 utilizando la métrica propuesta en el capítulo
cuatro. Dicha cantidad aparece en la ecuación de campo de Einstein.
En varias ocasiones fue necesario usar códigos simbólicos de las
ecuaciones de la relatividad general para comparar los resultados obtenidos.
Esto se hizo esencialmente con programas realizados en REDUCE 3.6, otros en
MATHEMATICA 3.0 y algunos más con MAPLE 5.1.
utilizando la métrica propuesta en el capítulo
cuatro. Dicha cantidad aparece en la ecuación de campo de Einstein.
En varias ocasiones fue necesario usar códigos simbólicos de las
ecuaciones de la relatividad general para comparar los resultados obtenidos.
Esto se hizo esencialmente con programas realizados en REDUCE 3.6, otros en
MATHEMATICA 3.0 y algunos más con MAPLE 5.1.




Next: INTRODUCCIÓN A LA TEORÍA
Up: Índice de Figuras
Previous: GLOSARIO
Índice General
enrique pazos
2000-09-27