Condensados Bose-Einstein

Utilizando la distribución de Bose-Einstein

$$\overline{n}_i=\frac 1{e^\alpha e^{\epsilon /kT}-1}=\frac 1{e^{\beta (-\mu +\varepsilon _i)}-1}=f_{be}(E)$$ (41)

al calcular el número total de partículas del sistema

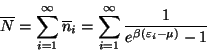$$\overline{N}=\sum\limits_{i=1}^\infty \overline{n}_i=\sum\limits_{i=1}^ \infty \frac 1{e^{\beta (\varepsilon _i-\mu )}-1}$$ (42)

y encontrando la densidad de estados de energía

$f(\varepsilon )d\varepsilon =\frac{V4\pi p^2}{h^3}\frac{dp}{d\varepsilon } d\varepsilon =\frac{V2\pi (2m)^{3/2}}{h^3}\varepsilon ^{1/2}d\varepsilon$

donde $\varepsilon =\frac{p^2}{2m}$

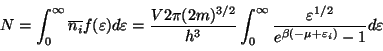$$N=\int_0^\infty \overline{n_i}f(\varepsilon )d\varepsilon \s... ...psilon ^{1/2}}{e^{\beta (-\mu +\varepsilon _i)}-1}d\varepsilon$$ (43)

donde para resolver la integral se hace la sustitución: $z= \varepsilon /kT$

$$\frac NV=\left( \frac{2\pi mkT}{h^2}\right) ^{3/2}\left( \frac 2{\sqrt{\pi } }\int_0^\infty \frac{z^{1/2}}{e^z-1}dz\right)$$ (44)

el potencial químico para un gas es siempre negativo, $\mu <0$ pero si se mantiene constante la parte derecha de la ecuación anterior, a medida que $T$ disminuye $\mu$ que es negativo deberá incrementarse. Sin embargo, el valor absoluto de $\mu$ decrece de manera tal que se define una temperatura mínima $T_c,$ donde el potencial aunque nunca llega a cero, es muy cercano a este valor. Entonces $\mu$ se desvanece desapareciendo así en la ecuación anterior. Sin embargo esto implica que existe una temperatura $T_c$ tal que el gas no puede ser enfriado a una densidad constante.

Evaluando la integral numéricamente:

$\left( \frac 2{ \sqrt{ \pi }} \int_0^ \infty \frac{ {z}^{1/2}}{e^{ {z} }-1}d {z}\right) = 2.\,6124$

y la fracción $\frac NV$ se convierte en:

$$\frac NV=2.61\left( \frac{2\pi mkT_c}{h^2}\right) ^{3/2}$$ (45)

Estas consideraciones son válidas para $T \geq T_c$ sin embargo para $T<T_c$ se necesita hacer ciertas modificaciones. Se sabe que a medida que la temperatura descienda, las partículas se aglomerarán en los estados más bajos de energía. A temperaturas altas no es un factor considerable el número de partículas en el nivel más bajo de energía. Sin embargo, a temperaturas bajas no es posible omitir este estado, puesto que contiene un número apreciable de partículas. Cuando se hace la generalización, a bajas temperaturas es necesario mantener el primer miembro de la integral, esto es $\varepsilon =0,$ (el estado base) que reescribiendo la ecuación 2.13 obtenemos:

$$N_{\varepsilon >0}=\frac 1{e^{-\beta (\mu )}-1}+\frac{V2\pi ... ...silon ^{1/2}}{e^{\beta (-\mu +\varepsilon _i)}-1} d\varepsilon$$ (46)

El primer término de esta ecuación corresponde a $N_1$ $(N=N_1+N_2+N_3+...N_p\,$que es equivalente a la Ec. 2.13) este es el número de partículas cuya energía y momentum no son cero. Sobre la temperatura $T_c$ el potencial químico no se desvanece y la ecuación 2.13  permanece igual. Para bajas temperaturas el número de partículas que tienen energía distinta de $0$ está dado por la ecuación anterior, nuevamente haciendo uso de $z= \varepsilon /kT$ y evaluando nuevamente la integral

$$N_{\varepsilon >0}=N\left( \frac T{T_c}\right) ^{3/2}$$ (47)

y el resto de partículas que se encuentran en el estado base con energía y momentum cero estará dado por:

$$\frac{N_1}N=1-\left( \frac T{T_c}\right) ^{3/2}$$ (48)

estas partículas se incrementan a medida que baja la temperatura. Debido a que estas partículas no tienen energía ni momentum, no contribuyen a la presión ni poseen viscosidad (la viscosidad es asociada al transporte de momentum). El aglomeramiento de partículas en este estado se conoce como condensado Bose-Einstein. Se caracteriza porque no hay una separación espacial en fases con diferentes propiedades. Tal como la presión en un vapor saturado depende únicamente de su temperatura. $T_c$ es conocida como la temperatura de condensación y un gas a temperaturas debajo de esta temperatura presenta una degeneración en energía.