Distribución de Bose-Einstein

Considerando un gas con un número fijo de partículas $N$ con energías $E_r$ que requiere el uso de estadísticas cuánticas para la descripción del mismo. Esto es, que sea un gas de partículas idénticas obedeciendo la estadística de Bose-Einstein (bosones).

$$N=\sum_in_i,\hspace{0.05in}E_{r}=\sum_in_i\varepsilon _i$$ (49)

donde $n_i$ corresponde al número de ocupación del estado asumiendolo desde cero hasta infinito con energías $\varepsilon _1\ll \varepsilon _2\ll ...\varepsilon _n$

Se utiliza la distribución de Gibbs o distribución macrocanónica. La descripción se hace a través de la función de macro partición del sistema (no confundir con $Z$ la función de partición para moléculas en un baño térmico) y recordando que el potencial químico está definido como: $\mu \equiv -T\frac{ \partial S_2}{\partial N_o}$.

$$\mathcal{Z}(T,V,\mu )\mathcal{\ =}\sum_{r}e^{-\beta (\mu N-E_{nr})}$$ (50)

además con la distribución de probabilidad normalizada (Gibbs)

$$p_{r}=\frac{e^{-\beta (\mu N-E_{r})}}{\mathcal{Z}}=p(n_{1,}n_{2...})$$ (51)

reescribiendo los exponenciales y sustituyendo en la función de macro partición utilizando

$$\mathcal{Z}_i=\sum_{_{n_i}}e^{\left[ -\beta (\mu -\varepsilon _i)n_i\right] }$$ (52)

y sustituyendo ahora en la función de probabilidad

$$\Pi _{i=1}^\infty \frac{e^{\left[ -\beta (\mu -\varepsilon _... ...i\right] }}{ \mathcal{Z}_i}=\Pi _{i=1}^\infty p_i(n_i)=p_{N_r}$$ (53)

lleva a que la distribución de probabilidad depende de un estado $i$ solamente. Significa que la probabilidad de encontrar $n_i$ partículas es independiente de los otros números de ocupación $n_j$ donde $j\neq i.$ Interpretando este resultado, se concluye que el estado de un sistema de partículas que no interactúan entre sí puede especificase en términos de los estados individuales. La energía del sistema es la suma de las energías individuales y es posible considerar un estado a la vez. $\cite{mandl}$

Además, debe cumplirse que la probabilidad esté normalizada

$$\sum\limits_{n_i}p_i(n_i)=1$$ (54)

para las estadísticas de Bose-Einstein, donde $n_i=0,1,2....$ la función de macro partición se convierte en una serie geométrica que converge solo si el exponencial es menor que 1, esto ocurre cuando $\mu <\varepsilon .$

$$\mathcal{Z}_i=\frac 1{1-e^{-\beta (\mu -\varepsilon _i)}}$$ (55)

ahora calculando el número medio de ocupación $(\overline{n}_i)$ del iésimo estado

$$\overline{n}_i=\frac 1{1-e^{-\beta (\mu -\varepsilon _i)}}=f_{be}(E) \hspace{0.2in} \textit{ distribuci\'{o}n BE}$$ (56)

generalizando para el número total de partículas en el sistema:

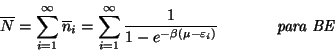$$\overline{N}=\sum\limits_{i=1}^\infty \overline{n}_i=\sum\li... ...-\beta (\mu -\varepsilon _i)} }\hspace{0.5in} \textit{para BE}$$ (57)