| (58) |
Utilizando la definición de fugacidad en función del
potencial químico
| (58) |
donde el potencial químico lo definiremos de tal manera que:
donde ![]() corresponde a la energía libre de Helmholtz. Sin
embargo, debido a que no se conoce el número exacto de partículas
del sistema macroscópico se introduce el ensemble macro
canónico. Con la condición de que los sistemas pueden tener
cualquier número de partículas y el número promedio de
partículas se determina por condiciones externas.
corresponde a la energía libre de Helmholtz. Sin
embargo, debido a que no se conoce el número exacto de partículas
del sistema macroscópico se introduce el ensemble macro
canónico. Con la condición de que los sistemas pueden tener
cualquier número de partículas y el número promedio de
partículas se determina por condiciones externas.
Ahora se considera un sistema con un número total de partículas ![]() tal que es posible hacer una subdivisión, de manera que se encuentren
tal que es posible hacer una subdivisión, de manera que se encuentren ![]() partículas en
partículas en ![]() y en
y en ![]() un número de partículas
un número de partículas ![]()
Es posible escribir la función de partición en función de la
energía libre de Helmholtz
![]() ya que
ya que
![]() . Es necesario que la
energía interna debe ser el promedio del hamiltoniano
. Es necesario que la
energía interna debe ser el promedio del hamiltoniano ![]() para el
ensemble y que la temperatura, presión y potencial químico tengan
valores definidos
para el
ensemble y que la temperatura, presión y potencial químico tengan
valores definidos ![]() respectivamente. La validez de estos
enunciados es evidente si se recuerda que la termodinámica es deducida
del ensemble canónico. Es posible aproximar la energía de Helmholtz
si
respectivamente. La validez de estos
enunciados es evidente si se recuerda que la termodinámica es deducida
del ensemble canónico. Es posible aproximar la energía de Helmholtz
si ![]() y
y ![]() a
a
| (59) |
y definimos la presión como:
| (60) |
Es posible definir a función de gran partición en
términos de la fugacidad ya definida. Esto facilita el cálculo de de
las funciones termodinámicas del sistema y será útil para
encontrar la ecuación de estado.
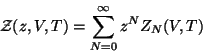 |
(61) |
Si se introduce la condición de que el volumen sea infinito tal que el
rango del número de partículas ![]() también lo sea,
también lo sea,
![]() al calcular la función de densidad que representa estados
descritos por las coordenadas y momenta
al calcular la función de densidad que representa estados
descritos por las coordenadas y momenta ![]() en el espacio
en el espacio ![]() ,
denotada por
,
denotada por ![]() Se integra esta función
Se integra esta función ![]() sobre las coordenadas y para un
sobre las coordenadas y para un ![]() dado, se suma sobre el rango de
dado, se suma sobre el rango de ![]()
![]() la ecuación de estado se escribe como
la ecuación de estado se escribe como
| (62) |
se determina el número medio de partículas
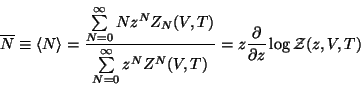 |
(63) |
y la energía interna
| (64) |
Cuando se toma en cuenta el carácter de la distribución
Bose-Einstein es necesario hacer las correcciones para tomar en cuenta la
distribución molecular. Esto conduce a que la ecuación de estado se
escribe como
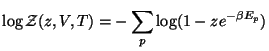 |
(65) | ||
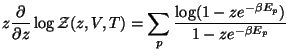 |
(66) |
| (67) |
enfatizando que la condensación ocurre únicamente cuando se conserva el número de partículas.