Parámetros de dispersión

La dispersión de partículas se puede descomponer en:

• ondas corridas (shifted waves) para el caso $l=0$,

• ondas planas (plane waves)

• ondas distorsionadas (distorted waves) donde en las soluciones $\psi _o$ no aparece un potencial $V(r).$ $\cite[25]{landau}$

La ventaja que presenta que los potenciales sean centrales es la conservación del momentum angular. Mientras el momentum angular se conserve es posible descomponer el análisis de la dispersión de las partículas incidentes. Se descompone en ondas dispersadas por el potencial, que actúa en un rango $a$ del centro del blanco (denominado longitud de dispersión). Esto lleva a una superposición de eigenestados de momentum angular, cada uno con un número cúantico $l$ definido.

De esta manera se analiza una partícula con energía $E$ y momentum dado por $p=\hbar k=\left( 2mE\right) ^{1/2}$ . De la aproximación semiclásica, $\cite[28]{landau}$ un parámetro de impacto $b$ (clásico) se identifica con el número cuántico del momentum angular $l.$

$$l+\frac 12\simeq kb$$ (68)

utilizando estos resultados, el momentum angular de la partícula será aproximadamente

$$L\simeq \hbar \left( l+\frac 12\right) \simeq \hbar l$$ (69)

de manera que será dispersada únicamente si

$$\hbar l<ap$$ (70)

para cumplir las condiciones del potencial, de manera que:

$$\hbar l<ap=a(2mE)^{1/2}$$ (71)

donde el máximo de partículas afectadas ocurre cuando

$$l_{\max }\geq kb$$ (72)

Para un potencial de corto alcance (rango $a$) donde $V(r)=0$ para $r>a,$ solo son dispersadas las partículas con parámetros de impacto $b$ menor que $a.$ Sin embargo, para una energía dada, solo algunas de las partículas serán dispersadas con ciertos valores de $l$ . Nos interesa en particular el caso de las ondas $s$ dispersadas, éstas se caracterizan por el número $l=0$ y que se producen a bajas energías. Al considerar nuevamente las soluciones para la ecuación de Schrödinger para la partícula libre.[20, 28] Reescribiéndolas en términos de $l,$ ya que para la onda $s$ se considera el caso $l=0$

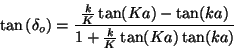$$\tan \left( \delta _o\right) =\frac{\frac kK\tan (Ka)-\tan (ka)}{1+\frac kK\tan (Ka)\tan (ka)}$$ (73)

y definiendo $\mathcal{L}$ como $\frac{d\psi (kr)/dr}{\psi (kr)}$ denominada la derivada logarítmica

$$\tan \left( \delta _o\right) \rightarrow K^{2l+1}\frac{r_m^{... ...+1)(1\cdot 3\cdot 5\cdot ...\cdot (2l-1))^2(l+\mathcal{L}r_m)}$$ (74)

que es producto de la solución de Schrödinger para la partícula libre. Al reemplazar el factor independiente de $K$ de la ecuación anterior y se denomina

$$\mathfrak{a} = \left( \frac{r_m^{2l+1}\left[ \left( l+1\righ... ...ot 3\cdot 5\cdot ...\cdot (2l-1))^2(l+\mathcal{L}r_m)}\right)$$ (75)

A medida de que $K$ $\rightarrow 0$ la solución se aproxima a:

$$\tan \left( \delta _l\right) \rightarrow \mathfrak{a}_lk^{2l+1}$$ (76)

para el valor de $l=0$ (ondas $s$) el valor $\mathfrak{a}_o$ es denominado longitud de dispersión. Similarmente, para $\mathfrak{a}_1$ es corresponde al volumen de dispersión.

Equivalentemente esta relación puede escribirse como:

$$\frac{1}{\mathfrak{a}_l}\rightarrow \cot \left( \delta _l\ri... ...c{1}{\mathfrak{a}_l}\rightarrow \cot \left( \delta _l\right) k$$ (77)

De estos resultados es evidente que los corrimientos de fase se desvanecen en $K=0.$ Se comprueba que existe un valor de energía bajo, que existe ùnicamente por la contribución de las ondas s.

El hecho de que las ondas sean esféricas, se justifica luego de calcular la componente radial de la densidad de corriente $j$. Usando el resultado de la mecánica cuántica para encontrar la densidad de corriente para una función de onda $\psi (r).$ $\cite[235]{mandlqm}$ Se aprovecha el hecho de que la función de onda depende de $r$ y para la onda que es positiva

$$j_r=\pm \frac{\hbar k}m\left\vert f(\theta ,\phi )\right\vert ^2\frac 1{r^2}$$ (78)

y la parte radial $\frac 1{r^2}$ nos justifica la interpretación de las ondas esféricas. La función $f(\theta ,\phi )$ es denominada amplitud de dispersión cuyo valor dado por la aproximación de Born (válido a altas energías)

$$f(\theta ,\phi )=\frac{-m}{2\pi \hbar }\int d^3re^{iK\cdot r}V(r)$$ (79)

Para encontrar la sección eficaz diferencial en el elemento de ángulo sólido $d\Omega$ se define como:

$$\sigma (\theta ,\phi )d\Omega =\frac{n(\theta ,\phi )d\Omega }I$$ (80)

El número de partículas dispersadas en el elemento de ángulo sólido en una dirección dada por unidad de tiempo es ( Esta notación es consistente con [22, 242]

$$n(\theta ,\phi )d\Omega =\frac{\hbar k}m\left\vert f(\theta ,\phi )\right\vert ^2d\Omega$$ (81)

Sabiendo que la normalización conduce a que el flujo incidente de partículas sea $\frac{\hbar k}m.$ Y además, debido a que el potencial presenta una simetría esférica, conlleva a que la onda incidente es simétrica alrededor del eje $z$. Esto implica que la sección eficaz dependerá únicamente del ángulo $\theta$

$$\sigma (\theta ,\phi )=\left\vert f(\theta )\right\vert ^2$$ (82)