Descripción: ecuación de onda

Al considerar un centro de dispersión fijo, representado por un potencial $V(r)$ y las partículas que viajan en la dirección $z$ se representan por las ondas planas

$$\psi _o(r)=e^{ikz}$$ (83)

Además, se impone que $\psi _o$ esté normalizada, de manera que representa una partícula por unidad de volumen. Entonces, ésta representa una solución a la ecuación de la partícula libre de Schrödinger.

$$\left( \nabla ^2+k^2\right) \psi _o(r)=\frac{2m}{\hbar ^2}V(r)\psi_o (r)$$ (84)

donde el número de onda $k$ está dado por: $k=(2mE/\hbar ^2)^{1/2}.$ La solución está sujeta a las condiciones de frontera tal que $\psi (r)\rightarrow \psi _o(r)=e^{ikz}$ a medida de que $V(r)\rightarrow 0.$ A medida de que se aleja del centro de dispersión, la onda se aproximará a la onda plana. Es decir que se desprecia el efecto de la interacción de Coulomb, debido precisamente a que se necesita que el potencial cumpla con $r\left( V(r)\right) \rightarrow 0$ a medida que $r\rightarrow \infty$ isotrópicamente.

De la solución a la ecuación de la partícula libre, a medida de que $r$ se incrementa, presenta soluciones que representan ondas esféricas (salientes del centro de dispersión con signo $+$, en dirección opuesta $-$) de la forma:

$$\frac 1re^{\pm ikr}f(\theta ,\phi )$$ (85)

Se necesita resolver la ecuación de Schrödinger para el caso de una partícula en estado estacionario

$$\left[ \frac{p^2}{2\mu }+V(r)\right] \psi (r)=E\psi (r)$$ (86)

lo que conduce a soluciones de la forma

$$\psi (r)=(2l+1)u(r)P_l\cos \theta$$

De la expansión de la onda plana en eigenestados de momentum

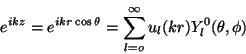$$e^{ikz}=e^{ikr \cos \theta }=\sum_{l=o}^{\infty} u_l(kr)Y_l^0(\theta ,\phi )$$ (87)

donde $Y_l^{0}(\theta ,\phi )$ se justifica porque en este caso no puede haber un eigenestado con $m\neq 0$ porque se asume una simetría azimutal [22, 246] Los coeficientes $u(k,r)$ toman la forma:

$$u_0(kr)=\int d\Omega Y_0^0(\theta ,\phi)e^{ikr \cos \theta }=(4 \pi )^{1/2} \frac{\mathrm{sen}(kr)}{kr}$$ (88)

utilizando $Y_0^{0}(\theta ,\phi )=\frac{1}{\sqrt{4 \pi }} \cite[682]{arfken}.$ Regresando a la expansión de la onda plana, se obtiene que es el producto de la superposición de la onda con $l=0$ (ondas $s$) y las ondas con $l>0$ tal que

$$e^{ikz}=(4\pi )^{1/2}\frac{\mathrm{sen}(kr)}{kr}\frac 1{\sqrt{4\pi }}=\frac{\mathrm{sen}(kr)}{ kr}+...\;\;\;(l>0)$$ (89)

al reescribir el $\mathrm{sen}(kr)$ de forma exponencial compleja $\cite[682]{arfken}$ la parte de la onda $s$ corresponde a:

$$\frac 1{2ik}\left( -\frac{e^{-ikr}}r+\frac{e^{ikr}}r\right)$$ (90)

resultado que fue interpretado como la superposición de dos ondas. Una que entra y otra que sale del centro de dispersión. Como es necesario que se mantenga el flujo de partículas en una dirección y en la otra, la amplitud de ambas ondas tiene el mismo valor absoluto. Este resultado es consecuencia de la conservación de momentum angular.

Tomando en consideración que el potencial distorsiona la onda plana en el estado dispersado, como una onda plana y una onda esférica $(\psi (r)\simeq e^{ikz}+\frac 1re^{ikr}f(\theta ,\phi )).$ Similarmente la onda $s$ dispersada también necesita agregar el término de la onda esférica dispersada a partir del blanco

$$\psi_0(r)\simeq \frac{\mathrm{sen}(kr)}{kr}+\frac 1re^{ikr}f... ...{-ikr}}{r} + \frac{e^{ikr}}{r} \left( 1+2ikf_0 \right) \right]$$ (91)

Pero de la condición de que los flujos de partículas (con $l=0)$ sean iguales, conduce a que en la ecuación anterior $\left( 1+2ikf_0 \right) =-1$ o que

$$\left\vert 1+2ikf_0 \right\vert =1$$ (92)

de esta manera $1+2ikf_0$ representa un factor de fase que puede expresarse como $\cite[246]{mandlqm}$

$$1+2ikf_0 =e^{2i\delta_0}$$ (93)

de donde $f_0=$ $\frac{e^{2i\delta _0 }-1}{2ik }$y el parámetro $\delta _0$ debe ser real y es denominado el corrimiento de fase de la onda s. Sustituyendo $f_0$ para las ondas $s$

$$\psi _0 (r)=e^{i\delta _0 }\frac{\mathrm{sen}(kr+\delta _0 )}{kr}$$ (94)

Se utiliza el resultado para bajas energías de $f_0=$ $\frac{e^{2i\delta _0 }-1}{2ik }$. Se complementa el resultado con la aproximaciòn de Born para altas energìas y se encuentra la sección eficaz diferencial, en términos de las amplitudes de dispersión

$$\sigma (\theta )d\Omega =\left\vert f_0 \right\vert ^2d\Omega =\frac{ d\Omega }{k^2}\mathrm{sen}^2\delta _0$$ (95)

$$\sigma _{tot} =\frac{4\pi }{k^2}\mathrm{sen}^2\delta _0$$ (96)

este resultado obviamente es menor o igual $\frac{4\pi }{k^2}$ , esto debido a que $\left\vert \mathrm{sen}\delta _0 \right\vert \ll 1.$ Estos resultados son del desarrollo cuando $l=0,$ o sea únicamente para las ondas $s$. Sin embargo, son válidos para los desarrollos de las otras ondas parciales , ya que si se sigue este con el factor $f_0 =\frac 1ke^{i\delta _0 }\mathrm{sen}\delta _0$ en la ecuación $\psi (r)\simeq e^{ikz}+\frac 1re^{ikr}f(\theta ,\phi ).$ La amplitud $f(\theta ,\phi )$ estará dada por

$$f(\theta ,\phi )=\frac{\sqrt{4\pi }}k\sum\limits_{l=0}^\inft... ...^{i\delta _l }\sin\delta _l Y _l ^0\left( \theta ,\phi \right)$$

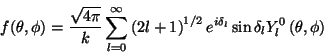
y la sección eficaz diferencial por unidad de ángulo sólido será dada por:

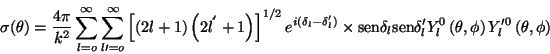$$\sigma (\theta )=\frac{4\pi }{k^2}\sum\limits_{l=o}^\infty \... ...theta ,\phi \right) Y^{\prime 0}_l \left( \theta ,\phi \right)$$ (97)

sin embargo, usando las propiedades de ortogonalidad de los armónicos esféricos la sección eficaz total

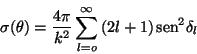$$\sigma (\theta )=\frac{4\pi }{k^2}\sum\limits_{l=o}^\infty \left( 2l+1\right) \mathrm{sen}^2\delta _l$$ (98)

resultado que se reduce a nuestro resultado anterior para $l=0.$ Si se tiene un pozo de potencial de forma que

$$V(r)= \left\{ \begin{array}{ll} -V_o,(V_o>0) & r<a \\ 0 & r>a \end{array} \right.$$ (99)

se requiere nuevamente la solución de la ecuación de Schrodinger que satisfaga la condición de frontera de que $\psi _0 (0)$ constante y distinto de 0 en el origen. Implica que

$$\left[ -\frac \hbar {2m}\nabla ^2+V(r)\right] \psi _0 (r)=E\psi _0 (r)$$ (100)

presenta las soluciones para ondas s $(\frac{e^{\pm iKr}}{r})$ donde $K=\left[ \frac{2m}{\hbar} (E+V_0)\right] ^{1/2}.$ Y las soluciones que satisfacen estas condiciones son

$$\psi _0 (r)=A\frac{\mathrm{sen}(Kr)}{Kr},\hspace{1in}r \geq a$$ (101)

recordando las soluciones obtenidas al utilizar el corrimiento de fase

$$\psi _o (r)=e^{i\delta _o}\frac{\mathrm{sen}(kr+\delta _o)}{kr}$$ (102)

Estas soluciones deben ser iguales en $r=a$, tal que la función y su derivada sean continuas en este punto $\psi _o (r)$ y $d(\psi _o(r))dr.$ Igualando las funciones a sus derivadas en $r=a,\tan (ka+\delta _o )=\frac kK\tan (Ka)$ despejando $\tan\left( \delta _o\right)$

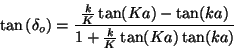$$\tan \left( \delta _o\right) =\frac{\frac kK\tan (Ka)-\tan (ka)}{1+\frac kK\tan (Ka)\tan (ka)}$$ (103)

De manera que es posible encontrar el $\mathrm{sen}\left( \delta _o\right)$ y por ende la sección eficaz, si solamente ocurre dispersión de onda $s$. En este caso la energía es suficientemente pequeña y $ka\ll 1.$ La relación $\hbar l<ap$ garantiza que solo habrá dispersión de onda s ($l$ es muy pequeño, o $0$). Así es posible aproximar $ka\approx \tan (ka)$

$$\tan\left( \delta _o\right) =\frac{ka\left[ \frac{\tan (Ka)}{Ka}-1\right]}{1+ ka^2\frac{\tan (Ka)}{Ka}}$$ (104)

la sección eficaz está dada por

$$\sigma _{tot}=\frac{4\pi }{k^2}\mathrm{sen}^2\delta _o$$ (105)

si $\tan\delta _o=0$ no existe la dispersión de onda $s$. Esto implica que $\tan (Ka)/Ka=1$.

Esto es conocido como el efecto Ramsauer-Townsend y ocurre en la dispersión de electrones lentos en átomos de gases raros. Cerca de 1eV las secciones eficaces presentan un mínimo y casi se desvanecen. En este caso las contribuciones de las otras ondas parciales ($l>0)$ no son significativas, haciendo válida la expansión en ondas parciales y la descripción del fenómeno en términos de ondas $s$.