



Next: Símbolos de Christoffel
Up: DE LA RELATIVIDAD ESPECIAL
Previous: Gravedad y relatividad especial
Índice General
Se tiene un sistema de coordenadas primado y uno no primado, tal que
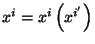 ; la cual es una función real,
univaluada y sus derivadas existen. En forma diferencial las ecuaciones son
; la cual es una función real,
univaluada y sus derivadas existen. En forma diferencial las ecuaciones son
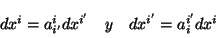 |
(2.11) |
donde
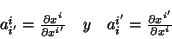 |
(2.12) |
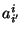 y
y
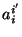 son los coeficientes de
transformación y cumplen con la propiedad
son los coeficientes de
transformación y cumplen con la propiedad
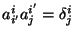 .
Un sistema de coordenadas es una manera de identificar puntos en el espacio.
Su propósito es nombrar puntos, el de la métrica es conectarlos
geométricamente. En el caso de un espacio plano, la distancia entre dos
puntos
.
Un sistema de coordenadas es una manera de identificar puntos en el espacio.
Su propósito es nombrar puntos, el de la métrica es conectarlos
geométricamente. En el caso de un espacio plano, la distancia entre dos
puntos
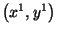 y
y
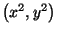 la
distancia es
la
distancia es
![$\left[ \left( x^{1}-x^{2}\right) ^{2}+\left(
y^{1}-y^{2}\right) ^{2}\right] ^{1/2}$](img203.gif) ; así, el espacio tiene asignada
una métrica. La métrica puede ser asignada diferencialmente mediante
; así, el espacio tiene asignada
una métrica. La métrica puede ser asignada diferencialmente mediante 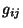 , el tensor métrico.
Si en un sistema de coordenadas el tensor métrico es
, el tensor métrico.
Si en un sistema de coordenadas el tensor métrico es
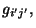 se cumple que
se cumple que
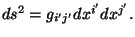 El tensor métrico se puede transformar con ayuda de
la ec. 2.12. Al hacer esto resulta que
El tensor métrico se puede transformar con ayuda de
la ec. 2.12. Al hacer esto resulta que
es decir,
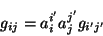 |
(2.14) |
En forma general, un tensor se tranforma de esta manera. Si una cantidad
dada se transforma de acuerdo a la ec. 2.14, entonces esa
cantidad es un tensor. [3] Este tipo de transformaciones se conoce
como transformaciones lineales.
La ec. 2.13 puede escribirse así:
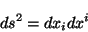 |
(2.15) |
donde
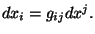 De esta manera se dice que
De esta manera se dice que 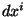 es un
intervalo contravariante y
es un
intervalo contravariante y 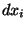 es un intervalo covariante . Se puede observar que mediante el tensor métrico es
posible subir o bajar (como en este caso) los índices de un vector o un
tensor.
es un intervalo covariante . Se puede observar que mediante el tensor métrico es
posible subir o bajar (como en este caso) los índices de un vector o un
tensor.




Next: Símbolos de Christoffel
Up: DE LA RELATIVIDAD ESPECIAL
Previous: Gravedad y relatividad especial
Índice General
enrique pazos
2000-09-27
![$\left[ \left( x^{1}-x^{2}\right) ^{2}+\left(
y^{1}-y^{2}\right) ^{2}\right] ^{1/2}$](img203.gif) ; así, el espacio tiene asignada
una métrica. La métrica puede ser asignada diferencialmente mediante
; así, el espacio tiene asignada
una métrica. La métrica puede ser asignada diferencialmente mediante