



Next: Tensor de Riemann, tensor
Up: DE LA RELATIVIDAD ESPECIAL
Previous: Símbolos de Christoffel
Índice General
Se considera que
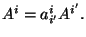 Tomando la derivada
ordinaria se tiene
Tomando la derivada
ordinaria se tiene
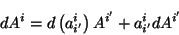 |
(2.20) |
si las componentes no cambian, entonces
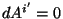 y
y 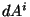 es
debido sólo al desplazamiento paralelo; por lo tanto
es
debido sólo al desplazamiento paralelo; por lo tanto
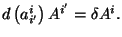 Entonces,
Entonces,
para un sistema estrellado,
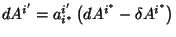 que al igualarlos da
que al igualarlos da
de esta última ecuación, se ve que la magnitud entre paréntesis
se transforma como un vector, por lo tanto es un vector, designado como
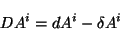 |
(2.23) |
Esta diferencia da el cambio en el vector debido a las características
curvilíneas del sistema de coordenadas, dejando el cambio real
en el vector. La ec. 2.23 se puede escribir
como [3]
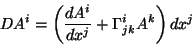 |
(2.24) |
la cantidad entre paréntesis es un tensor mixto llamado derivada
covariante. La ec. 2.24 puede escribirse de la forma
siguiente:
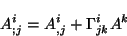 |
(2.25) |
donde el punto y coma representa la derivada covariante. De la misma forma,
para un vector covariante se tiene
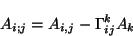 |
(2.26) |
Todos los conceptos anteriores se pueden generalizar fácilmente para la
geometría del espacio-tiempo, simplemente haciendo las sumatorias
sobre cuatro dimensiones.




Next: Tensor de Riemann, tensor
Up: DE LA RELATIVIDAD ESPECIAL
Previous: Símbolos de Christoffel
Índice General
enrique pazos
2000-09-27