



Next: Descomposición en 3+1
Up: FORMALISMO ADM EN RELATIVIDAD
Previous: FORMALISMO ADM EN RELATIVIDAD
Índice General
La formulación de la teoría de la relatividad general tiene como
concepto central el principio de equivalencia. Este principio
implica que las ecuaciones deben escribirse en forma covariante, o sea,
independiente del sistema de coordenadas. Una característica de las
ecuaciones de Einstein es que algunas de ellas representan constricciones en
las variables dinámicas, las cuales están relacionadas con las
identidades de Bianchi,
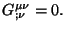 Separar las ecuaciones
dinámicas de aquellas que presentan constricciones se hace difícil
debido a la misma forma covariante de expresar las ecuaciones.
Una forma de analizar la dinámica de la relatividad general consiste en
verla como un problema de Cauchy, es decir, analizar la dinámica como la
evolución de una hipersuperficie tridimensional donde estén definidos
los campos. Esta manera de formular la relatividad general fue desarrollada
por R. Arnowitt, S. Deser y C. W. Misner [8]. Este formalismo se
conoce por las iniciales de sus autores como la formulación ADM de la
relatividad general y se desarrolló a principios de los años 60.
La obtención de las ecuaciones de Einstein a través de la
formulación ADM tiene su forma más clara usando el principio
variacional, el cual involucra la construcción de una cantidad
invariante llamada lagrangiano. En relatividad general, la
constucción de invariantes se basa en el escalar de curvatura
Separar las ecuaciones
dinámicas de aquellas que presentan constricciones se hace difícil
debido a la misma forma covariante de expresar las ecuaciones.
Una forma de analizar la dinámica de la relatividad general consiste en
verla como un problema de Cauchy, es decir, analizar la dinámica como la
evolución de una hipersuperficie tridimensional donde estén definidos
los campos. Esta manera de formular la relatividad general fue desarrollada
por R. Arnowitt, S. Deser y C. W. Misner [8]. Este formalismo se
conoce por las iniciales de sus autores como la formulación ADM de la
relatividad general y se desarrolló a principios de los años 60.
La obtención de las ecuaciones de Einstein a través de la
formulación ADM tiene su forma más clara usando el principio
variacional, el cual involucra la construcción de una cantidad
invariante llamada lagrangiano. En relatividad general, la
constucción de invariantes se basa en el escalar de curvatura 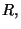 integrado sobre un tetra-volumen. Se busca que esta cantidad sea, como su
nombre lo indica, un invariante en cualquier sistema de coordenadas. Dado
que una función escalar cumple con este requerimiento,
integrado sobre un tetra-volumen. Se busca que esta cantidad sea, como su
nombre lo indica, un invariante en cualquier sistema de coordenadas. Dado
que una función escalar cumple con este requerimiento, 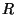 será un
invariante. La propuesta inmediata sería tomar a
será un
invariante. La propuesta inmediata sería tomar a 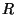 como una densidad lagrangiana, de tal forma que al efectuar la integral
como una densidad lagrangiana, de tal forma que al efectuar la integral 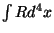 se obtenga una función denominada acción. Esta propuesta
tiene el inconveniente de que
se obtenga una función denominada acción. Esta propuesta
tiene el inconveniente de que 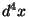 no es un invariante. Para corregir este
defecto, se introduce el factor
no es un invariante. Para corregir este
defecto, se introduce el factor 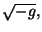 donde
donde 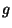 es el determinante de
la métrica en cuatro dimensiones. Se puede decir entonces, que el
invariante que determina una densidad lagrangiana para la parte
geométrica de las ecuaciones de Einstein será
es el determinante de
la métrica en cuatro dimensiones. Se puede decir entonces, que el
invariante que determina una densidad lagrangiana para la parte
geométrica de las ecuaciones de Einstein será
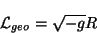 |
(3.1) |
El principio variacional para la teoría gravitacional fue postulado por
Hilbert, quien lo expresó de la forma [5]
donde la densidad lagrangiana está dada por la ec. 3.1. Al
realizar la variación de esta densidad lagrangiana con respecto a los
campos de la métrica 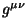 se obtiene la parte izquierda de la
ec. 2.38, que es la ecuación de campo en el vacío
se obtiene la parte izquierda de la
ec. 2.38, que es la ecuación de campo en el vacío
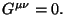
![\begin{displaymath}
\frac{\delta \mathcal{L}_{geo}}{\delta g^{\mu \nu }}=\sqrt{-g}\left[ R_{\mu
\nu }-\frac 12g_{\mu \nu }R\right]
\end{displaymath}](img287.gif) |
(3.3) |
Para obtener la parte derecha de la ec. 2.38 se necesita una
densidad lagrangiana de materia apropiada y así tener completa esta
ecuación. La densidad lagrangiana total estará compuesta entonces de
dos partes
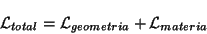 |
(3.4) |
la obtención del lagrangiano de materia se verá en la sección
3.5.
La construcción de un hamiltoniano a partir de este punto, implica la
construcción de los momentos canónicos conjugados a las variables
dinámicas, es decir, a las diez componentes del tensor métrico,
tomando la derivada parcial de la densidad lagrangiana respecto de las
velocidades. Para hacer esto, es necesario privilegiar una
coordenada o una dirección en el espacio-tiempo. La forma de hacerlo es
considerar rebanadas del espacio-tiempo, de tal manera que cada una de estas
rebanadas sea una hipersuperficie de tres dimensiones con una métrica
positiva definida en ella. Si a cada una de estas hipersuperficies se le
identifica con un parámetro 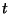 y se pide que ninguna de ellas se
interseque, entonces se puede considerar la evolución de las mismas como
el cambio de éstas en el parámetro
y se pide que ninguna de ellas se
interseque, entonces se puede considerar la evolución de las mismas como
el cambio de éstas en el parámetro 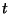 y cubrir así todo el
espacio-tiempo. La trimétrica
y cubrir así todo el
espacio-tiempo. La trimétrica 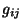 definida en cada hipersuperficie
depende del tiempo y se puede considerar como una variable dinámica.
[9]
De aquí en adelante, la trimétrica
definida en cada hipersuperficie
depende del tiempo y se puede considerar como una variable dinámica.
[9]
De aquí en adelante, la trimétrica 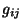 se diferencia de la
métrica original
se diferencia de la
métrica original
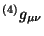 por los índices y
además, para disminuir la ambigüedad, se le antepone el número de
dimensiones. La métrica
por los índices y
además, para disminuir la ambigüedad, se le antepone el número de
dimensiones. La métrica 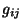 tiene seis componentes, esto implica que
se deben definir otras cuatro variables para tener un total de diez, que es
el número de componentes del tensor métrico original
tiene seis componentes, esto implica que
se deben definir otras cuatro variables para tener un total de diez, que es
el número de componentes del tensor métrico original
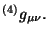 Estas nuevas variables son las funciones
Estas nuevas variables son las funciones 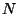 y
y 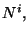 llamadas función lapse y función shift,
respectivamente. La función lapse está relacionada con la separación
entre cada hipersuperficie. La función shift tiene que ver con el
movimiento de un punto al pasar de una hipersuperficie a otra.
Lo que sigue ahora es reescribir el elemento de línea
llamadas función lapse y función shift,
respectivamente. La función lapse está relacionada con la separación
entre cada hipersuperficie. La función shift tiene que ver con el
movimiento de un punto al pasar de una hipersuperficie a otra.
Lo que sigue ahora es reescribir el elemento de línea 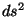 en
funcion de la trimétrica
en
funcion de la trimétrica 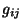 y las variables
y las variables 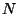 y
y 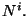 Posteriormente, se procede a formular la acción gravitacional en
términos de la nuevas variables. La acción estará dada como
Posteriormente, se procede a formular la acción gravitacional en
términos de la nuevas variables. La acción estará dada como
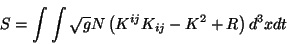 |
(3.5) |
donde 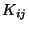 es la curvatura extrínseca. La no dependencia de la
densidad lagrangiana de las derivadas temporales de
es la curvatura extrínseca. La no dependencia de la
densidad lagrangiana de las derivadas temporales de 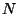 y
y 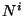 , permite
considerarlas como variables dinámicas no relevantes. Esto quiere decir
que las verdaderas variables dinámicas son las seis componentes de
, permite
considerarlas como variables dinámicas no relevantes. Esto quiere decir
que las verdaderas variables dinámicas son las seis componentes de 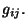 Ahora se puede construir la densidad hamiltoniana
Ahora se puede construir la densidad hamiltoniana 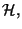 a partir de
la densidad lagrangiana. Para esto se definen los momentos canónicos
conjugados a
a partir de
la densidad lagrangiana. Para esto se definen los momentos canónicos
conjugados a 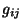 de la forma
de la forma
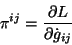 |
(3.6) |
donde el punto sobre 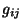 indica derivada respecto de
indica derivada respecto de 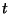 . La cantidad
. La cantidad 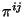 se trabaja como una densidad tensorial. Con esto, la densidad
hamiltoniana está dada por
se trabaja como una densidad tensorial. Con esto, la densidad
hamiltoniana está dada por
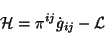 |
(3.7) |
esta densidad hamiltoniana tiene la forma
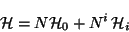 |
(3.8) |
Con la densidad hamiltoniana se puede escribir la acción donde las
variables dinámicas sean 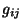 y
y 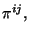 la expresión es
la expresión es
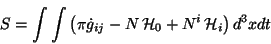 |
(3.9) |
La ecuaciones de movimiento se obtienen al hacer las variaciones respecto de
las diferentes variables. [9]




Next: Descomposición en 3+1
Up: FORMALISMO ADM EN RELATIVIDAD
Previous: FORMALISMO ADM EN RELATIVIDAD
Índice General
enrique pazos
2000-09-27