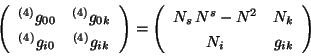Next: Principio variacional
Up: FORMALISMO ADM EN RELATIVIDAD
Previous: Introducción
Índice General
Se consideran dos hipersuperficies las cuales se etiquetan con los nombres 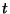 y
y 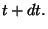 Un punto en la hipersuperficie
Un punto en la hipersuperficie 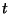 está identificado con
otro punto en la hipersuperficie
está identificado con
otro punto en la hipersuperficie 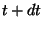 . La correspondencia entre estos se
hace a través de un vector que une dichos puntos y que a su vez da la
distancia entre los mismos. Para lograr esto se necesita lo siguiente:
. La correspondencia entre estos se
hace a través de un vector que une dichos puntos y que a su vez da la
distancia entre los mismos. Para lograr esto se necesita lo siguiente:
- El conocimiento de la trimétrica
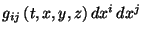 en la hipersuperficie
en la hipersuperficie 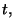 la cual da la distancia entre dos
puntos situados sobre ella.
la cual da la distancia entre dos
puntos situados sobre ella.
- La trimétrica
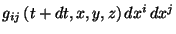 en
la hipersuperficie
en
la hipersuperficie 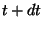 .
.
- Una fórmula para la distancia propia entre las
hipersuperficies, la cual está dada por
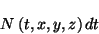 |
(3.10) |
donde 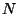 es la función lapse. La expresión anterior da la longitud
de un vector perpendicular a
es la función lapse. La expresión anterior da la longitud
de un vector perpendicular a 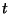 , que se extiende entre las dos
hipersuperficies.
, que se extiende entre las dos
hipersuperficies.
- Una fórmula para la distancia (en la hipersuperficie
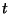 ) a la
que se encuentran los puntos que se corresponden mutuamente, que es
) a la
que se encuentran los puntos que se corresponden mutuamente, que es
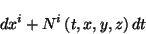 |
(3.11) |
donde 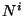 es la función shift. El término
es la función shift. El término 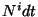 representa el
desplazamiento que se manifiesta cuando los orígenes de los sistemas de
coordenadas de las hipersuperficies no están unidos por un vector
ortogonal a ambas.
representa el
desplazamiento que se manifiesta cuando los orígenes de los sistemas de
coordenadas de las hipersuperficies no están unidos por un vector
ortogonal a ambas.
El intervalo invariante entre
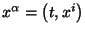 y
y
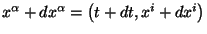 está dado por
está dado por
Puede verse que en el caso de 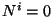 el elemento de línea tendrá
contribuciones de la distancia sobre la hipersuperficie base
el elemento de línea tendrá
contribuciones de la distancia sobre la hipersuperficie base 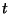 y el tiempo
propio, pues la evolución de las hipersuperficies es meramente temporal.
Comparando la ec. 3.12 con la métrica en cuatro dimensiones
se llega a
y el tiempo
propio, pues la evolución de las hipersuperficies es meramente temporal.
Comparando la ec. 3.12 con la métrica en cuatro dimensiones
se llega a
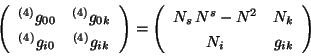 |
(3.13) |
En la ecuación anterior, 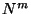 son las componentes contravariantes de la
función shift. La relación entre las covariantes está dada por
son las componentes contravariantes de la
función shift. La relación entre las covariantes está dada por
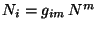 . La relación inversa se expresa como
. La relación inversa se expresa como
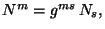 donde
donde 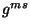 es el inverso de
es el inverso de 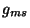 y cumplen con
y cumplen con
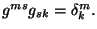 La cuatro-métrica contravariante correspondiente es [5]
La cuatro-métrica contravariante correspondiente es [5]
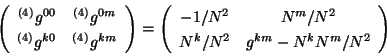 |
(3.14) |




Next: Principio variacional
Up: FORMALISMO ADM EN RELATIVIDAD
Previous: Introducción
Índice General
enrique pazos
2000-09-27