



Next: Solución para un caso
Up: APLICACIÓN DEL FORMALISMO ADM
Previous: Ecuaciones de movimiento
Índice General
La ec. 4.46 tiene la forma de una ecuación onda con fuente. El
problema es que la variable independiente aparece en el lado derecho de la
ecuación, lo cual hace que no se le pueda encontrar una solución
exacta. Lo mismo se puede decir de la ec. 4.48, la cual es una
ecuación en derivadas parciales, no homogenea y no lineal.
La ec. 4.49 se puede escribir la forma
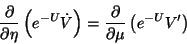 |
(4.50) |
esta ecuación manifiesta que las derivadas parciales de las expresiones
entre paréntesis deben ser iguales. Esta condición se satisface si
tales cantidades tiene la forma
donde 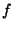 y
y 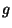 son funciones arbitraria cuyo argumento debe ser de la forma
son funciones arbitraria cuyo argumento debe ser de la forma
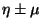 , y
, y 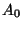 y
y 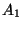 son constantes de integración.
Conociendo la función
son constantes de integración.
Conociendo la función 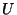 se podría resolver las ecuaciones
anteriores para encontrar
se podría resolver las ecuaciones
anteriores para encontrar 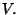 Del tensor de energía-momentum se obtienen dos ecuaciones
más. Estas provienen de la propiedad
Del tensor de energía-momentum se obtienen dos ecuaciones
más. Estas provienen de la propiedad
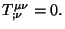 La ec.
4.17 da el tensor de energía-momentum para un fluido
perfecto. Al tomar la derivada covariante e igualarla a cero se obtienen las
siguientes expresiones
La ec.
4.17 da el tensor de energía-momentum para un fluido
perfecto. Al tomar la derivada covariante e igualarla a cero se obtienen las
siguientes expresiones
De la condición planteada por la ec. 4.18 se obtiene que
en base a la expresión anterior se propone que
donde 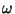 es una nueva variable desconocida. Sustituyendo estas
expresiones para
es una nueva variable desconocida. Sustituyendo estas
expresiones para 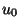 y
y 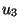 en la ec. 4.54 se tiene lo siguiente
en la ec. 4.54 se tiene lo siguiente
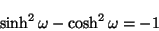 |
(4.56) |
esta es una identidad que se cumple para cualquier valor real del
parámetro 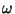 .
Estas ecuaciones aportan información acerca del comportamiento de los
campos . Sin embargo su forma es muy compleja para poder extraer la
información de ellas. Debido a esto y a la dificultad de encontrar una
solución a las ecuaciones presentadas anteriormente se tratará con un
problema más sencillo que el original, esto se detalla en la siguiente
sección.
.
Estas ecuaciones aportan información acerca del comportamiento de los
campos . Sin embargo su forma es muy compleja para poder extraer la
información de ellas. Debido a esto y a la dificultad de encontrar una
solución a las ecuaciones presentadas anteriormente se tratará con un
problema más sencillo que el original, esto se detalla en la siguiente
sección.




Next: Solución para un caso
Up: APLICACIÓN DEL FORMALISMO ADM
Previous: Ecuaciones de movimiento
Índice General
enrique pazos
2000-09-27