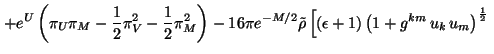Next:Ecuaciones
de EinsteinUp:APLICACIÓN
DEL FORMALISMO ADMPrevious:Lagrangiano
de la geometríaÍndice
General
Lagrangiano de la materia
En esta parte se obtendrá la contribución a la densidad lagrangiana
cuando se tiene una fuente. Para resolver el conjunto de ecuaciones diferenciales
parciales 3.32,
3.33,
3.34,
con el fin de obtener la densidad lagrangiana de materia, se considera
un tensor de energía-momentum para un fluido perfecto [10]
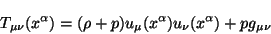 |
(4.17) |
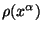 y
y 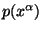 son la densidad de materia y la presión de la misma, respectivamente.
Ambas cantidades son dependientes de las coordenadas. En esta ecuación,
son la densidad de materia y la presión de la misma, respectivamente.
Ambas cantidades son dependientes de las coordenadas. En esta ecuación, 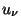 es la velocidad del fluido, la cual cumple con la condición
es la velocidad del fluido, la cual cumple con la condición
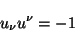 |
(4.18) |
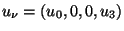 .
Partiendo de la ec. 4.18
se puede despejar una de ellas en función de la otra, para lo cual
se tiene que
.
Partiendo de la ec. 4.18
se puede despejar una de ellas en función de la otra, para lo cual
se tiene que
De esta ecuación se puede encontrar 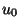 en función de
en función de 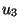 ,
siendo la expresión general
,
siendo la expresión general
![\begin{displaymath}u_0=\frac{-2g^{0m}u_m\pm \left[ \left( 2g^{0m}u_m\right) ^2......0}\left(1+g^{km}u_ku_m\right) \right] ^{\frac 12}}{2g^{00}}\end{displaymath}](img449.gif) |
(4.20) |
![\begin{displaymath}u_0=N^mu_m\pm \left\{ \left( N^mu_m\right) ^2+N^2\left[ 1+\......frac{N^k\,N^m}{N^2}\right) u_ku_m\right] \right\} ^{\frac 12}\end{displaymath}](img450.gif) |
(4.21) |
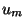 significará sólo la componente 3 de la velocidad, es decir
significará sólo la componente 3 de la velocidad, es decir 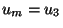 .
Al resolver la ec. 3.34,
se elige la norma para las funciones como
.
Al resolver la ec. 3.34,
se elige la norma para las funciones como 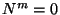 ,
con lo cual la ecuación anterior se reduce a
,
con lo cual la ecuación anterior se reduce a 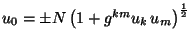 .
Además, la velocidad contravariante se obtiene de la manera usual,
subiendo el índice con la métrica contravariante
.
Además, la velocidad contravariante se obtiene de la manera usual,
subiendo el índice con la métrica contravariante 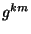 ,
es decir,
,
es decir, 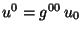 ,
obteniendo que
,
obteniendo que
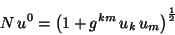 |
(4.22) |
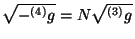 .
Se considera también que la ecuación de estado del fluido
de materia sea tipo barotrópica, en la cual se cumple que
.
Se considera también que la ecuación de estado del fluido
de materia sea tipo barotrópica, en la cual se cumple que 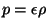 ,
donde
,
donde 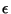 es una constante. Escribiendo explícitamente la ec. 3.34
se tiene lo siguiente
es una constante. Escribiendo explícitamente la ec. 3.34
se tiene lo siguiente
Haciendo el cambio de variable 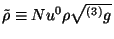 y utilizando la ec. 4.22
el primer término del integrando queda de la siguiente manera
y utilizando la ec. 4.22
el primer término del integrando queda de la siguiente manera
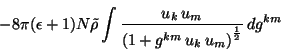 |
(4.24) |
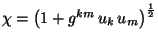 ,
se observa que
,
se observa que 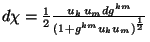 ,
con lo cual esta primera integral es
,
con lo cual esta primera integral es
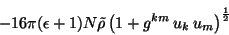 |
(4.25) |
 .
De esto se ve que la variación
.
De esto se ve que la variación 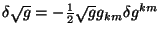 ,
de aquí se observa que el segundo integrando es el diferencial de
la raíz cuadrada del determinante de la trimétrica. Con esto
se llega a que el segundo término es
,
de aquí se observa que el segundo integrando es el diferencial de
la raíz cuadrada del determinante de la trimétrica. Con esto
se llega a que el segundo término es
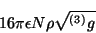 |
(4.26) |
![\begin{displaymath}\mathcal{L}_{mat}=-16\pi N\tilde{\rho}\left[ (\epsilon +1)\......\left(1+g^{km}\,u_{k}\,u_{m}\right) ^{-\frac{1}{2}}\right]\end{displaymath}](img471.gif) |
(4.27) |
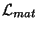 con respecto a
con respecto a 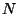 ,
se parte de la ec. 3.32,
con la misma norma
,
se parte de la ec. 3.32,
con la misma norma 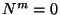 ,
con esto se tiene que
,
con esto se tiene que
![\begin{displaymath}\frac{1}{2}N^{3}\frac{\partial \mathcal{L}_{mat}}{\partial ......t{^{(3)}g}\left[ (\epsilon +1)u_{0}^{2}-N^{2}\epsilon \right]\end{displaymath}](img473.gif) |
(4.28) |
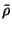 ,
se llega de nuevo a la ec. 4.27,
por lo cual la variación con respecto a
,
se llega de nuevo a la ec. 4.27,
por lo cual la variación con respecto a 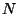 no da nuevos elementos a la densidad lagrangiana. Para la variación
de
no da nuevos elementos a la densidad lagrangiana. Para la variación
de 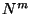 se toma la ecuación
se toma la ecuación
![\begin{displaymath}\frac{1}{2}N^{2}\frac{\partial \mathcal{L}_{mat}}{\partial ...... (\epsilon+1)u_{k}u_{m}+\epsilon g_{km}\right] N^{k}\right]\end{displaymath}](img475.gif) |
(4.29) |
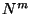 ,
los términos cuadráticos o de otro orden son despreciados.
La contribución a la densidad lagrangiana proveniente de la variación
de los
,
los términos cuadráticos o de otro orden son despreciados.
La contribución a la densidad lagrangiana proveniente de la variación
de los 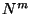 queda de la siguiente forma
queda de la siguiente forma
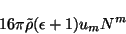 |
(4.30) |
Uniendo el resultado obtenido anteriormente con aquel de la ec. ![[*]](crossref.png) ,
se llega a que la densidad lagrangiana total para este problema es
,
se llega a que la densidad lagrangiana total para este problema es




Next:Ecuaciones
de EinsteinUp:APLICACIÓN
DEL FORMALISMO ADMPrevious:Lagrangiano
de la geometríaÍndice
General
enrique pazos 2000-09-27
![]() en función de
en función de ![]() ,
siendo la expresión general
,
siendo la expresión general
![\begin{displaymath}u_0=\frac{-2g^{0m}u_m\pm \left[ \left( 2g^{0m}u_m\right) ^2......0}\left(1+g^{km}u_ku_m\right) \right] ^{\frac 12}}{2g^{00}}\end{displaymath}](img449.gif)
![\begin{displaymath}u_0=N^mu_m\pm \left\{ \left( N^mu_m\right) ^2+N^2\left[ 1+\......frac{N^k\,N^m}{N^2}\right) u_ku_m\right] \right\} ^{\frac 12}\end{displaymath}](img450.gif)
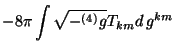
![$\displaystyle -8\pi \int N\sqrt{^{(3)}g}\rho \left[ (\epsilon +1)u_{k}\,u_{m}+\epsilon\,g_{km}\right] d\,g^{km}$](img462.gif)
![]() y utilizando la ec. 4.22
el primer término del integrando queda de la siguiente manera
y utilizando la ec. 4.22
el primer término del integrando queda de la siguiente manera
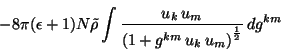
![[*]](crossref.png) ,
se llega a que la densidad lagrangiana total para este problema es
,
se llega a que la densidad lagrangiana total para este problema es
![$\displaystyle \pi _{U}\dot{U}+\pi _{V}\dot{V}+\pi _{M}\dot{M}%%+Ne^{M/2}\left...... \prime }+2U^{\prime }M^{\prime }-\left( V^{\prime }\right)^{2}\right] \right.$](img480.gif)