


Next: The Zeldovich approximation
Up: Describing the inhomogeneities of
Previous: Describing the inhomogeneities of
A particularly simple case occurs when dealing with very small
inhomogeneities. This is the case either at very early epochs or at
the present time, when considering sufficiently large scales, so that
the variance of the galaxy number counts is much less than unity. In
this regime, 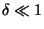 and
and 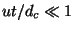 ,
,
 being the expansion time-scale and
being the expansion time-scale and  the characteristic
coherence length of the fluctuation field. This enables us to neglect
in eqs.(12) all the non-linear terms, to get
the characteristic
coherence length of the fluctuation field. This enables us to neglect
in eqs.(12) all the non-linear terms, to get
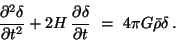 |
(13) |
Note that the linear approximation amounts to assuming no phase
coupling, so that fluctuation modes at different wavelengths evolve
independent of each other.
In the case of a flat Universe with 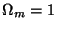 , no cosmological
constant, and matter dominated expansion, the Friedmann equations
give
, no cosmological
constant, and matter dominated expansion, the Friedmann equations
give
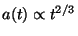 , and eq.(13) has the general solution
, and eq.(13) has the general solution
 |
(14) |
This solution essentially says that perturbation evolution is given by
the superposition of a growing and a decaying mode, that becomes
rapidly negligible as expansion goes on. It is interesting to note
that
 grows at the same rate as the scale factor
grows at the same rate as the scale factor
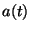 . This is nothing but the consequence of the similarity between
the gravitational collapse time-scale,
. This is nothing but the consequence of the similarity between
the gravitational collapse time-scale,
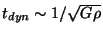 ,
and the expansion time-scale,
,
and the expansion time-scale,
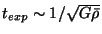 , that
occurs in the
, that
occurs in the 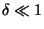 case. This result is valid both for a
flat Universe and for an open Universe (
case. This result is valid both for a
flat Universe and for an open Universe (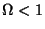 ) at sufficiently
early times, when
) at sufficiently
early times, when
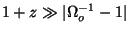 and the spatial
curvature can be neglected. However, in the last case, at later times
the cosmic expansion rate increases, so that the fluctuation growing
stops and their amplitudes are frozen. Thus, in order to allow
observed structures to be formed, a not too low density parameter is
required.
and the spatial
curvature can be neglected. However, in the last case, at later times
the cosmic expansion rate increases, so that the fluctuation growing
stops and their amplitudes are frozen. Thus, in order to allow
observed structures to be formed, a not too low density parameter is
required.
As the typical fluctuation amplitude approaches unity at a given
scale, phase coupling terms in eqs.(12) start playing a role and
the linear approximation breaks down. In this case, a rigorous treatment for
inhomogeneity evolution has not yet been derived, although different
prescriptions have been developed to get hints about non-linear aspects of
gravitational clustering.
As a direct approach, one can perturbatively expand eqs.(![[*]](file:/usr/local/lib/latex2html/icons/crossref.png) )
in terms of increasing order in
)
in terms of increasing order in 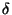 and try to solve the system
order by order. While linear equations preserve initial Gaussianity,
the inclusion of the lowest-order non-linear terms gives rise to a non
vanishing skewness of the fluctuation probability distribution
[25], that is the signature of non-Gaussian statistics. This
approximation is expected to hold in the
and try to solve the system
order by order. While linear equations preserve initial Gaussianity,
the inclusion of the lowest-order non-linear terms gives rise to a non
vanishing skewness of the fluctuation probability distribution
[25], that is the signature of non-Gaussian statistics. This
approximation is expected to hold in the
 regime,
while in the
regime,
while in the  regime the convergence of the perturbative
expansion series is no longer guaranteed.
regime the convergence of the perturbative
expansion series is no longer guaranteed.



Next: The Zeldovich approximation
Up: Describing the inhomogeneities of
Previous: Describing the inhomogeneities of
Waleska Aldana Segura
2001-01-16
![]() , no cosmological
constant, and matter dominated expansion, the Friedmann equations
give
, no cosmological
constant, and matter dominated expansion, the Friedmann equations
give
![]() , and eq.(13) has the general solution
, and eq.(13) has the general solution
![]() )
in terms of increasing order in
)
in terms of increasing order in ![]() and try to solve the system
order by order. While linear equations preserve initial Gaussianity,
the inclusion of the lowest-order non-linear terms gives rise to a non
vanishing skewness of the fluctuation probability distribution
[25], that is the signature of non-Gaussian statistics. This
approximation is expected to hold in the
and try to solve the system
order by order. While linear equations preserve initial Gaussianity,
the inclusion of the lowest-order non-linear terms gives rise to a non
vanishing skewness of the fluctuation probability distribution
[25], that is the signature of non-Gaussian statistics. This
approximation is expected to hold in the
![]() regime,
while in the
regime,
while in the ![]() regime the convergence of the perturbative
expansion series is no longer guaranteed.
regime the convergence of the perturbative
expansion series is no longer guaranteed.