


Next: The linear approximation
Up: THE LARGE-SCALE STRUCTURE OF
Previous: The standard cosmological model
Cosmic inhomogeneities are usually described by the
fluctuation field
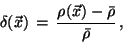 |
(7) |
where 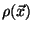 is the density of the Universe at the point
is the density of the Universe at the point  .
A popular statistical characterization of the inhomogeneities in the
distribution of cosmic structures is provided by
the
two-point correlation function,
.
A popular statistical characterization of the inhomogeneities in the
distribution of cosmic structures is provided by
the
two-point correlation function, 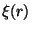 , which describes the expected excess
fluctuations with respect to a uniform distribution:
, which describes the expected excess
fluctuations with respect to a uniform distribution:
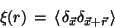 |
(8) |
where the symbol
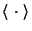 indicates the average over all the pairs of points at separation
indicates the average over all the pairs of points at separation 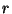 .
Its Fourier transform is the power spectrum
.
Its Fourier transform is the power spectrum
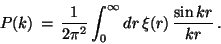 |
(9) |
If clustering is isotropic, then 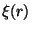 and
and 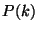 depend only on
the modulus of the separation- and wave-vectors, respectively. The
power spectrum of the observed galaxy and cluster distributions
contains formally the same amount of information as
depend only on
the modulus of the separation- and wave-vectors, respectively. The
power spectrum of the observed galaxy and cluster distributions
contains formally the same amount of information as 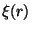 , although
the practical computation of the two quantities is differently
affected by the systematics of redshift surveys.
, although
the practical computation of the two quantities is differently
affected by the systematics of redshift surveys.
Another important statistical characterisation is provided by the
variance, 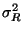 , of the mass density fluctuations within a
sphere of radius
, of the mass density fluctuations within a
sphere of radius 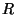 :
:
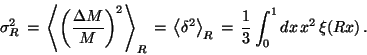 |
(10) |
Galaxy surveys show that for normal galaxies the variance in the
galaxy number counts is about unity for
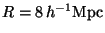 [7,21]. For this reason, it is customary to specify the
normalisation of the power spectrum at this scale, so that
[7,21]. For this reason, it is customary to specify the
normalisation of the power spectrum at this scale, so that
 provides the
so-called galaxy biasing with respect to the dark matter
distribution. Therefore, by definition, the galaxy biasing provides a
measure of the difference between the distribution of the observable
light and the distribution of the unseen cosmic dark matter.
provides the
so-called galaxy biasing with respect to the dark matter
distribution. Therefore, by definition, the galaxy biasing provides a
measure of the difference between the distribution of the observable
light and the distribution of the unseen cosmic dark matter.
Observations of the large-scale distribution of cosmic structures
shows that the two-point correlation function for both galaxies and
galaxy clusters can be well approximated by a power law,
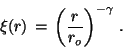 |
(11) |
Although the slope
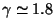 is quite simila
i.e. the correspondence between background and physical space-time)
in which fluctuation measurements are performed. In this case, a
proper gauge-invariant description of fluctuation evolution is
required and several prescriptions have been proposed by different
authors (see ref.[24] for a recent review on this
subject). At the present time, all the scales relevant for clustering
studies are are well inside the horizon. However, since perturbation
wavelengths scale with the redshift as
is quite simila
i.e. the correspondence between background and physical space-time)
in which fluctuation measurements are performed. In this case, a
proper gauge-invariant description of fluctuation evolution is
required and several prescriptions have been proposed by different
authors (see ref.[24] for a recent review on this
subject). At the present time, all the scales relevant for clustering
studies are are well inside the horizon. However, since perturbation
wavelengths scale with the redshift as
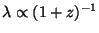 and the horizon as
and the horizon as
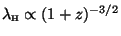 ,
the typical scale of galaxy clustering,
,
the typical scale of galaxy clustering,
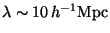 , crosses
the horizon at
, crosses
the horizon at 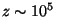 , roughly corresponding to the epoch of
matter-radiation equality. Thus, a gauge invariant treatment is
required when studying the formation of density fluctuations relevant
to the present observed clustering. Here we adopt a purely Newtonian
treatment, which is adequate to follow the perturbation evolution
after recombination, when structure formation starts.
, roughly corresponding to the epoch of
matter-radiation equality. Thus, a gauge invariant treatment is
required when studying the formation of density fluctuations relevant
to the present observed clustering. Here we adopt a purely Newtonian
treatment, which is adequate to follow the perturbation evolution
after recombination, when structure formation starts.
Passing to the Fourier representation of the density fluctuation
field, the system (![[*]](file:/usr/local/lib/latex2html/icons/crossref.png) ) becomes
) becomes
Eqs. (12) and (![[*]](file:/usr/local/lib/latex2html/icons/crossref.png) ) can be equivalently used as the
non-linear systems describing the evolution of cosmic density fluctuations.
In the following we will describe some approximations that
have been proposed in order to get hints about the nature of gravitational
clustering. In the next Chapter we will discuss the use of cosmological
N-body simulations as a tool to follow in detail the non-linear dynamics
implied by eqs.(12).
) can be equivalently used as the
non-linear systems describing the evolution of cosmic density fluctuations.
In the following we will describe some approximations that
have been proposed in order to get hints about the nature of gravitational
clustering. In the next Chapter we will discuss the use of cosmological
N-body simulations as a tool to follow in detail the non-linear dynamics
implied by eqs.(12).
Subsections



Next: The linear approximation
Up: THE LARGE-SCALE STRUCTURE OF
Previous: The standard cosmological model
Waleska Aldana Segura
2001-01-16
![]() , of the mass density fluctuations within a
sphere of radius
, of the mass density fluctuations within a
sphere of radius ![]() :
:
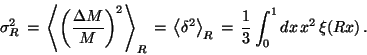
![]() ) becomes
) becomes