


Next: Non-baryonic models
Up: The spectrum of primordial
Previous: The spectrum of primordial
In order to follow the evolution of fluctuations of baryonic matter, let us
consider the second of eqs.(![[*]](file:/usr/local/lib/latex2html/icons/crossref.png) ), with the inclusion of a pressure
term:
), with the inclusion of a pressure
term:
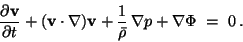 |
(22) |
Accordingly, the linearized equation for the evolution of the 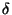 field in Fourier space reads
field in Fourier space reads
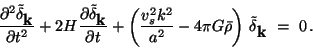 |
(23) |
Here
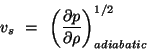 |
(24) |
is the adiabatic sound speed in a medium with equation of state 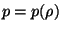 .
In eq.(23) we can define the critical Jeans wavelength
.
In eq.(23) we can define the critical Jeans wavelength
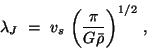 |
(25) |
which discriminates between two different regimes for the perturbation
evolution. For fluctuation modes with wavelength
 ,
the pressure contribution can be neglected and the linear solution of
eq.(14) is recovered. Viceversa, for
,
the pressure contribution can be neglected and the linear solution of
eq.(14) is recovered. Viceversa, for
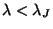 the gravitational term becomes negligible and the solution
oscillates. Thus, while fluctuations on a scale greater than the Jeans
length are not pressure-supported and are able to grow by gravity, at
scales below
the gravitational term becomes negligible and the solution
oscillates. Thus, while fluctuations on a scale greater than the Jeans
length are not pressure-supported and are able to grow by gravity, at
scales below 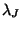 the fluctuations behave like oscillating
sound waves.
the fluctuations behave like oscillating
sound waves.
If 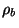 is the average baryon density, we can define
a baryon Jeans mass scale,
is the average baryon density, we can define
a baryon Jeans mass scale,
 |
(26) |
which is the mass of the smallest baryonic fluctuation that is able to
grow. Before recombination, at a redshift
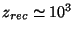 , matter and
radiation are tightly coupled by Thomson scattering. In this regime they
behave like a single fluid with
, matter and
radiation are tightly coupled by Thomson scattering. In this regime they
behave like a single fluid with
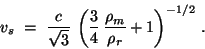 |
(27) |
Since matter-radiation equality occurs at
 , the Jeans mass just before recombination is
, the Jeans mass just before recombination is
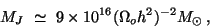 |
(28) |
of the same order of the mass of a supercluster. After recombination,
however, photons are no longer coupled to matter, so that the equation of
state rapidly changes and the baryonic component behaves like a monoatomic
gas with
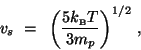 |
(29) |
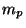 being the proton mass. At the recombination temperature
being the proton mass. At the recombination temperature
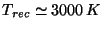 , it corresponds to a Jeans mass
, it corresponds to a Jeans mass
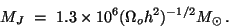 |
(30) |
Thus, although before recombination the Jeans mass involves scales of
superclusters, after matter and radiation decouple it drops by several
orders of magnitude to the value of the mass of globular clusters, and
fluctuations on small scales are able to start growing again.
It is worth comparing the Jeans mass before recombination with the baryon
mass contained inside the Hubble radius
 .
According to eq.(27), it is
.
According to eq.(27), it is
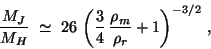 |
(31) |
so that, until radiation dominates, the Jeans mass exceeds the mass inside the
horizon and all the subhorizon fluctuations are constrained not to grow.
A further characteristic scale, which enters in the spectrum of baryon
fluctuations, is due to the collisional damping occurring just before
recombination. As recombination is approached, the coupling between
radiation and baryons becomes no longer perfect and the photon mean free
path starts increasing. Thus, photons can diffuse more easily from
overdensities carrying with them matter, to which they are however still
quite tightly coupled. The final effect is to damp fluctuations below the
scale which corresponds to the distance travelled by a photon in an expansion
time-scale. This is known as Silk damping [29] and an accurate
evaluation of the smoothing mass scale in the post-recombination baryon
spectrum [10] gives
 |
(32) |
which obviously depends on the baryon density parameter 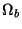 . The
Silk damping increases by several orders of magnitude the mass-scale of
the smallest fluctuation, which starts growing after recombination,
smaller scale perturbations being heavily suppressed.
. The
Silk damping increases by several orders of magnitude the mass-scale of
the smallest fluctuation, which starts growing after recombination,
smaller scale perturbations being heavily suppressed.
Although the simplicity of
a purely baryonic model is rather attractive, nevertheless it suffers from
a number of serious problems, which makes it extremely unlikely. Even
without referring to the difficulty of reconciling the predictions based
on primordial nucleosynthesis,
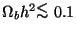 , with both
dynamical estimates of the mean cosmic density and the inflationary
prejudice
, with both
dynamical estimates of the mean cosmic density and the inflationary
prejudice 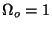 , the baryonic spectrum gives too large
fluctuations at the scale of 10-20
, the baryonic spectrum gives too large
fluctuations at the scale of 10-20
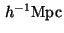 , with respect to what observed for
the galaxy distribution. Even more, a purely baryonic model is ruled out
since it predicts too high CMB temperature fluctuations with respect to
current detections.
, with respect to what observed for
the galaxy distribution. Even more, a purely baryonic model is ruled out
since it predicts too high CMB temperature fluctuations with respect to
current detections.



Next: Non-baryonic models
Up: The spectrum of primordial
Previous: The spectrum of primordial
Waleska Aldana Segura
2001-01-16
![]() is the average baryon density, we can define
a baryon Jeans mass scale,
is the average baryon density, we can define
a baryon Jeans mass scale,
![]() .
According to eq.(27), it is
.
According to eq.(27), it is
![]() , with both
dynamical estimates of the mean cosmic density and the inflationary
prejudice
, with both
dynamical estimates of the mean cosmic density and the inflationary
prejudice ![]() , the baryonic spectrum gives too large
fluctuations at the scale of 10-20
, the baryonic spectrum gives too large
fluctuations at the scale of 10-20
![]() , with respect to what observed for
the galaxy distribution. Even more, a purely baryonic model is ruled out
since it predicts too high CMB temperature fluctuations with respect to
current detections.
, with respect to what observed for
the galaxy distribution. Even more, a purely baryonic model is ruled out
since it predicts too high CMB temperature fluctuations with respect to
current detections.