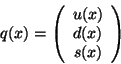Next: Unitarity Limit
Up: Examples
Previous: Examples
The hadronic current can be divided in one part corresponding to
conservation of strageness
 and in another which changes
strangeness
and in another which changes
strangeness
 :
:
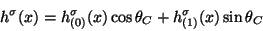 |
(83) |
where the mixing angle 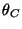 is constant and is called Cabbibo angle.
This angle was introduced in order to take into account the fact that
the reactions with
is constant and is called Cabbibo angle.
This angle was introduced in order to take into account the fact that
the reactions with
 have much less amplitude than the ones
preserving strtangeness. Universality in the hadronic world is then written:
have much less amplitude than the ones
preserving strtangeness. Universality in the hadronic world is then written:
The phenomenology indicates that each one of the parts of (85)
has a vectorial and an axial component, namely
that is, has the structure (V-A) as in the leptonic case.
As a complete theory of the strong interactions of hadrons is not
avaliable, it is not possible to give a simple expression of the
hadronic current in terms of operators for hadrons.
Nevertheless we can go deeper in the level of elementarity and take
the quark model (then it will be the basis of the quark theory : QCD).
The model of quarks comes from the hypothesis that the hadrons
are bound states of quarks 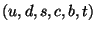 .
.
In order to present the usual phenomenology we can restrict
ourselves to a model with only light quarks 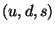 . We have then a
unitary internal symmetry of flavor,
. We have then a
unitary internal symmetry of flavor, 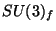 . Under this symmetry, the
quark triplet
. Under this symmetry, the
quark triplet
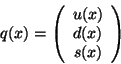 |
(88) |
is transformed as
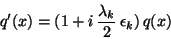 |
(89) |
where
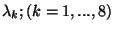 are the
are the 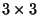 matrices of
matrices of 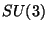 .
If the masses of
quarks are equal, the equation of motion of the free quarks is:
.
If the masses of
quarks are equal, the equation of motion of the free quarks is:
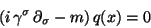 |
(90) |
It is then found a conserved vector current
 |
(91) |
and a non conserved axial current
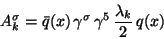 |
(92) |
because
 |
(93) |
In terms of the currents so defined, the electromagnetic current is
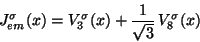 |
(94) |
meanwhile the weak components with  and
and 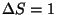 are:
are:
The Cabbibo hypothesis for the hadronic current is written
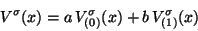 |
(99) |
with
 and
and
 . Due to the fact that
the only invariant under
SU(3) is
. Due to the fact that
the only invariant under
SU(3) is
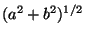 , it results that the condition
, it results that the condition
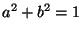 (Cabbibo universality) is also invariant,
but as
(Cabbibo universality) is also invariant,
but as 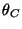 is experimentally fixed in
is experimentally fixed in
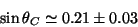 |
(100) |
one inmediatelly concludes that there is a breaking of 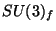 .
.



Next: Unitarity Limit
Up: Examples
Previous: Examples
root
2001-01-22
![]() and in another which changes
strangeness
and in another which changes
strangeness
![]() :
:
![]() .
.
![]() . We have then a
unitary internal symmetry of flavor,
. We have then a
unitary internal symmetry of flavor, ![]() . Under this symmetry, the
quark triplet
. Under this symmetry, the
quark triplet